“概率值”的意思、起源，概率值是由谁提出的-心理学-情感百科-依恋情感网

网站首页情感咨询情感美文情感百科情感生活学习充电旧版美文

标题	概率值
类别	心理学
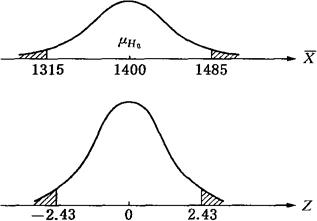
释义	【概率值】拼译：probability value 一译“概值”、“P值”。假设检验术语。分单侧概率值与双侧概率值两类。(1)单侧概率值，又分右侧概率值和左侧概率值。对于任何要检验的零假设H₀，H₀的右侧概率值是指“若H₀为真，样本统计量大于或等于实际观测值”的概率，H₀的左侧概率值是指“若H₀为真，样本统计量小于或等于实际观测值”的概率，两者均可写成P_r。如某总体X～N(μ，σ²)，其中σ²=(350)²，而μ未知。现欲检验的假设是H_0：μ=1400；H_1：μ＞1400。这属于右侧检验问题。现随机抽取n=100的样本，算得样本算术平均数=1485。检验统计量是Z===，在H₀成立的条件下，Z服从标准正态分布。在=1485时，Z==2．43。可查表得P_r(Z≥2．43)=P_r(≥1485)=0．0075。这就是检验H₀的概率值。它说明“Z≥2．43”或“≥1485”的概率只有0．0075，这是很小的可能性。若H₀是对的，要大于或等于1485是非常困难的。然而现在=1485，这个事实与H₀是严重不符的，可以拒绝H₀。(2)双侧概率值，指“若H₀真，统计量向双尾偏离至少到观测值之外”的概率，用P_r表示。上例中，若假设是H_0：μ=1400；H_1：μ≠1400，由于Z分布的对称性，有P_r(Z≥2．43)=P_r(Z≤一2．43)=0．0075。于是概率值等于P_r(｜Z｜≥2．43)=0．0075+0．0075=0．015。下面是由统计量和Z的分布表示的概率值。
随便看	黄宗羲黄帝黄庭坚黄建中黄教黄梨洲黄榦黄生黄石龙黄绾黄缭黄老黄老之术黄老学派黄老道黄老道德之术黄道周黄遵宪黄金分割黄金律黄钺黄震黄马、骊牛，三黎尔黎曼 preextration pre extration preextrusion equipment pre extrusion equipment pre extrusion punch PREF pref. prefab brick panel prefab clean room prefab cold storage prefab compound unit prefab construction method prefab form prefab garage prefab girder floor 情感散文答题技巧模板范文是什么意思阿兵哥的情书是什么意思静夜独思情感散文是什么意思玉哥哥情感语录是什么意思情书雪景是什么意思夫妻情感共鸣的散文作品是什么意思交错时空浪漫情书是什么意思情书有没有片尾歌曲是什么意思友情感悟散文是什么意思兄妹情感散文精选文章阅读是什么意思情书认错文案短句是什么意思袁隆平情感语录短句图片是什么意思乘坐火车旅行情感散文是什么意思包含张敏复出的情书的词条是什么意思收到太多情书是什么意思分手后，男人多久会找新欢前任说还爱你，但是为什么不复合呢前任有了新欢还频繁找你，该怎么办最高深的挽回秘诀，是这两个字微信被对方拉黑怎么挽回在一起越久，挽回越容易前任什么时候最想复合什么时候可以约前任见面经常吵架的情侣，最终会分手吗为什么男人总是对你冷暴力分手后男人是怎么想的为什么你发的朋友圈前任都不看分手后怎么让对方主动联系你异地恋女朋友提分手我不同意，怎么挽回老公因为一个游戏要和我离婚，怎么办秋季养生：探索灸疗方案，找回身心和谐秋季养生菜品推荐 \| 丰富多样的菜名秋季美容食物，让你焕发自信！秋季女性养生食品推荐秋季养生护理的五大方面秋季养生必备：药浴的7种方法秋季养生知识大揭秘！快来了解秋季健康保养的要点打造苗条身材，秋季减肥养生食谱推荐秋季养生汤品推荐，给你一个健康的季节秋季如何戴口罩养生保健？助您健康度过秋天秋季调养身体的方法大全——增强免疫力，预防感冒秋季养生水果有哪些好处与推荐秋季养生甜汤品种推荐，滋补佳品助你保健秋季养生鸡汤的七款经典配方，让你暖心又滋补秋季养生: 深秋滋补，预防三高

依恋情感网情感百科知识大全收录了49620条情感类百科知识词条，覆盖心理学、哲学、美学等领域，基本涵盖了日常生活中常见问题的详细解释，是情感生活的有利工具。