【两独立样本中位数相等检验】
拼译：test for equality of medians based on two independent samples
假设检验的一种。用于检验来自两个独立变量Y1与Y2(它们可以是类别、顺序或等距变量)的两样本中位数是否相等。它是“两独立样本总体比例相等检验”的直接应用。以Y1和Y2均为等距变量为例。记M1与M2分别为两变量的中位数，欲检验的假设是H0：M1=M2=M0；H1：M1≠M2。对两变量进行随机观测，得到两个独立样本，样本容量分别为n1与n2。将两个样本混合排序，并求得混合样本的中位数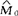
。记X1是来自Y1的样本中大于
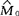的样品个数，X2是来自Y2的样本中大于
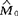的样品个数。再记Pr(X1＞
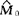)=p1，Pr(X2＞
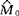)=p2，于是上面关于中位数相等的假设等价于这一假设：H0：p1=p2=
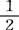；H1：p1≠p2。进而，运用两独立样本总体比例相等比例相等检验的方法。参见“两独立样本总体比例相等检验”。
- 蔡九峰
- 蔡仪
- 蔡元培
- 蔡元定
- 蔡和森
- 蔡墨
- 蔡孑民
- 蔡梅罗
- 蔡沈
- 蔡邕
- 蕅益
- 蕴涵
- 蕴涵式
- 蕴涵怪论
- 《无元哲学》
- 《无名论》
- 《无形学院》
- 《无意识哲学》
- 《无政府主义之平等观》
- 《无政府主义还是社会主义?》
- 《无神论》
- 《无能子》
- 《日内瓦宣言》
- 《日常生活批判》
- 《日本道德论》
- polyterpene resin
- Polyterpenoid
- polyterpenoids
- poly tert butyl crotonate
- polyterus bichir
- polytetradecamethylene carbonate
- polytetradecamethylene formal
- polytetradecanoic anhydride
- polytetrafiuoroethylene
- polytetrafluor ethylene
- polytetrafluorethylene
- polytetrafluoroethene
- polytetrafluoroethylene
- polytetrafluoroethylene aqueous dispersion
- polytetrafluoroethylene bearing, PTFE bearing
- 情感语录账号还值得去做吗是什么意思
- 感动的情感散文是什么意思
- 邂逅情感散文赏析是什么意思
- 夏雨情感散文是什么意思
- 秦腔散文作者情感是什么意思
- 情感散文作业设计案例分析是什么意思
- 散文中情感类作品名称大全是什么意思
- 赋子泽情书是什么意思
- 陕西游记散文情感是什么意思
- 有哪些好听的情感语录女生是什么意思
- 钢琴词《情书》是什么意思
- 情书翻车图片大全是什么意思
- 抒发爱家情感的散文是什么意思
- 庄子寄托丰富情感的散文是什么意思
- 情感语录望乡经典是什么意思
- 感情生活有基础，爱情才会锦上添花
- 何家劲：此生最爱一人，62岁仍未婚单身
- 如果一个异性很直接了当的说想跟你谈恋爱，怎么办？
- 成年人在恋爱里到底能有多直接？
- 我妈帮我照顾孩子竟要收我5万元，丈母娘是这么说的......
- 婚姻感情语录：人们都认为男人有力量,其实,男人的力量说到底还要归属女人
- 婚姻法规定夫妻感情破裂的标准丨怎么挽回破裂的婚姻
- 安倍昭惠与安倍晋三，结婚35年膝下无子
- 恋爱时两个人一起做哪些事可以快速增进感情？
- 爱情中爱与被爱哪个更重要一些？
- 女朋友pua我的表现有哪些呢？如何脱离女朋友的pua？
- 发现男人出轨最理智的做法是什么？别总手撕小三！
- 中国“最惨女星”曝光：被逼整容后惨遭遗弃？
- 车与车总是相撞，人与人却总是相让
- 婚姻幸福的“头号杀手”——婚外恋
- O血型女生减肥应该知道这些知识！
- O血型女眼中的异性魅力
- O型血的人如何在恋爱中获得幸福？
- 恋爱成功秘诀！O血型人该怎么做？
- 适合O血型人自律打卡的计划
- 你是O血型人？这些习惯一定要改
- O型血的女孩子有哪些性格特点？
- O型血恋爱中常见问题有哪些？你中招了吗？
- O型血的人在婚姻中需要注意什么？
- 爱情攻略：O型血如何收获甜甜的爱情
- O型血的7大特点，你中了几条？
- O型血的人婚姻事业和谁比较搭
- 哪种恋爱方式会击中O型血的心
- 陷入爱情的O型血人要注意什么
- O型血人适合哪些工作？