“主成分分析”的意思、起源，主成分分析是由谁提出的-心理学-情感百科-依恋情感网

网站首页情感咨询情感美文情感百科情感生活学习充电旧版美文

标题	主成分分析
类别	心理学
释义	【主成分分析】拼译：principal component analysis 多元统计分析的一种。研究如何通过变量的少数几个线性组合来解释这些变量的相关结构。1933年霍特林建立。若p个标准化相关变量Z₁，Z₂，…，Z_p的线性组合Y₁=b₁₁Z₁+…+b_1pZ_p，…，Y_p=b_p1Z₁+…+b_ppZ_p，且Y₁，Y₂，…，Y_p满足以下两个条件：(1)Y_i的系数向量为单位长，即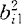+…+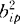=1，i=1，…，p；(2)Y₁，Y₂，…，Y_p的方差达到最大且互不相关，则Y₁，Y₂，…，Y_p被称为相关变量Z₁，Z₂，…，Z_p的主成分。第一主成分Y₁是一切系数为单位长的线性组合中方差最大者，第二主成分Y₂是一切系数为单位长且与Y₁不相关的线性组合中方差最大者，依次类推，第k主成分Y_k是一切系数为单位长且与前k－1个主成分不相关的线性组合中方差最大者。设λ₁≥λ₂≥…≥λ_p≥0是Z₁，Z₂，…，Z_p的相关矩阵R的特征根，e₁，e₂，…，e_p为相应的标准正交化特征向量。可以证明，第一主成分Y₁的系数向量是e₁，方差为λ₁，第二主成分Y₂的系数向量是e₂，方差为λ₂。一般地，第k主成分Y_k的系数向量是e_k，方差为λ_k，即Y_k=e_k1Z₁+e_k2Z₂+…+e_kpZ_p，k=1，2，…，p，式中e_k=(e_k1，e_k2，…，e_kp)′。且对于方差有如下结果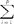λ_i=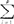Var(Y_i)=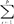Var(Z_i)=p，从而第k主成分的方差占变量总方差的比例为λ_k／p。若前m个主成分的方差之和占总方差的比例很大(如超过0．8)，则可用它们近似解释原来变量的变化情况，即主成分分析的思想。主成分分析可作为其他多元统计的中间环节。当变量较多且彼此相关时，用少数重要的主成分代替原来的变量，可用于回归分析、聚类分析等。
随便看	非条件反射非标准化测验非正式沟通非正式测验非正式组织非正式群体非法需要非洲心理学史非特定性被害人非特异因素非特异投射系统非理性主义非理性信念非理性信念问卷非理性机能非社会化－攻击性儿童非程序化决策非系统性观察非线性回归非结构式访谈非结构性Q分类非联想学习非自然语言系统非营利组织非行少年 wire fencing wire fencing, electrified wire ferrule wire figure, contour figure wire file wire fillet wire fillet clothing wire filter wire filter cloth wire finder wire finger splint wire fix wire fixation wire flame spray gun wire flame spraying 云雾缭绕情感语录图片高清是什么意思情感语录文案配音对话录音是什么意思古诗文表达情感方式是什么意思情书日本歌是什么意思斜坡艾青诗选赏析表达情感是什么意思截取学生情书是什么意思朗读文章3分钟散文情感是什么意思用景色表达情感的词语是什么意思心情感恩文案短句干净是什么意思小班艺术表达自己情感教案是什么意思情感语录段子女版是什么意思云云情感语录霸气文案女生是什么意思有优美情感语录的书籍是什么意思热门情感语录故事图片大全是什么意思中外爱情书籍是什么意思马云分享的一个受人欢迎的秘诀人生那么长，善待自己最重要 14岁的初三女孩小敏，大量吞服母亲的精神药物为了辅导孩子做作业，有位妈妈竟然跳了河让孩子学会吃苦、在苦中磨练意志李佳琦花1.3亿买房上了热搜贩卖人口绝不是一个孤立的事件和一个已婚男人在一起，没想到被他骗了生女儿是赔钱货，有本事生出儿子呀您没坐错位，但您坐错了车无论谁打电话找我都说我不在家有多少男人半夜起来给孩子喂奶难道你把我养大，就是为了照顾哥哥的吗明星没有了个性，还是那个你喜欢的明星吗陈数，才是优雅女人的典范开扒烂桃花比正桃花还旺的生肖，实惨快戳！9月份12生肖财运暴涨秘诀前方高能，12生肖4月运势提前报！ 2020年感情甜蜜婚姻幸福的生肖盘点11月爱情事业双丰收的四生肖九月好运连连的生肖top4，快来看！不可错过！八月份12生肖转运指南下半年这几个生肖终于逆袭，超爽夏至来袭！十二生肖避祸必看tips 喜大普奔，七月运势回暖的生肖！戳！七月份十二生肖财运暴涨秘诀六月桃花最旺的生肖TOP4，是你吗？六月贵人运大旺的生肖们，开挂了 12生肖如何才能在新一年收获满满喜大普奔！五月运势回暖的生肖

依恋情感网情感百科知识大全收录了49620条情感类百科知识词条，覆盖心理学、哲学、美学等领域，基本涵盖了日常生活中常见问题的详细解释，是情感生活的有利工具。