【混合类内协方差矩阵】
拼译:covariance matrix of pooled within-group
一译“混合组内协方差矩阵”,亦称“混合样本内协方差矩阵”。矩阵的一种。在多元统计中,将来自不同类或不同组的样本离差矩阵SS(i)综合起来得到的矩阵。它实际是各个样本的协方差矩阵的加权平均,可作为各样本来自的各总体(即各类)的综合协方差矩阵的估计。在判别分析、均值假设检验等方法中都有直接应用。若两个一元总体X1~N(μ1,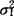 ),X2~N(μ2,
),X2~N(μ2,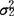 )满足方差齐性,即
)满足方差齐性,即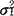 =
=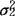 =σ2,为对假设“H0:μ1=μ2”作检验,在未知σ2时,可用检验统计量t=
=σ2,为对假设“H0:μ1=μ2”作检验,在未知σ2时,可用检验统计量t=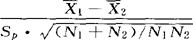 。在H0成立时,t服从t(N1+N2-2)分布。式中N1,
。在H0成立时,t服从t(N1+N2-2)分布。式中N1,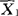 是来自总体X1的样本大小和均值,N2,
是来自总体X1的样本大小和均值,N2,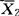 是来自总体X2的样本大小和均值。再记
是来自总体X2的样本大小和均值。再记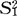 与
与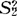 是分别来自两个总体的样本方差,则上面的
是分别来自两个总体的样本方差,则上面的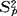 =
=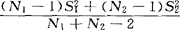 =
=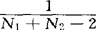 [
[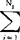 (X1i
(X1i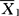 )2+
)2+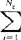 (X2i-
(X2i-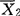 )2]就是两个样本的混合方差,它是公共方差σ2的无偏估计。在p维情况,若记
)2]就是两个样本的混合方差,它是公共方差σ2的无偏估计。在p维情况,若记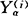 为来自第i类(总体)的随机样本中的第α个样品(α=1,2,…,ni;i=1,2,…,k)。各样本的均值向量是
为来自第i类(总体)的随机样本中的第α个样品(α=1,2,…,ni;i=1,2,…,k)。各样本的均值向量是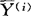 =
=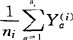 (i=1,2,…,k)。各样本的离差矩阵(即离差平方和矩阵)是SS(i)=
(i=1,2,…,k)。各样本的离差矩阵(即离差平方和矩阵)是SS(i)=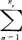 (
(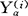 -
-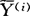 )(
)(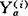 -
-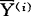 )′则k个类(总体)的样本的混合类内协方差矩阵为
)′则k个类(总体)的样本的混合类内协方差矩阵为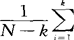 SS(i)=
SS(i)=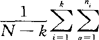 (
(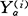 -
-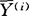 )(
)(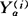 -
-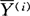 )′。它反映k个类的类内变异的情况。式中的N=
)′。它反映k个类的类内变异的情况。式中的N=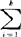 ni。参见“样本协方差矩阵”。
ni。参见“样本协方差矩阵”。
- driver education
- drive reduction
- drive-reduction theory
- driver information system
- driver's behavior model
- driver's fatigue
- driver's motional vision
- driver's psychological burden
- driver's reaction
- drive stimulus
- drive theory
- driving adaptability
- driving adaptability test
- driving attention
- driving capacity
- driving decision
- driving efficacy
- driving environment
- driving excitement
- driving expectation
- driving experimental vehicle
- driving failure
- driving habit
- driving illusion
- driving imitation experiment
- test of general ability
- test of goodness of fit
- test of habitual characteristics
- test of hardness drop by heating
- test of hearing threshold
- test of homogeneity
- test of homogeneity of varianc
- test of humoral function
- test of hypothesis
- test of identifying restriction
- test of independence
- test of independencecy
- test of independency
- test of inducing or stimulating disease location
- Test of intelligence
- 谁,把青春耗在暗恋里?是什么意思
- 谁许了谁 此生不悔是什么意思
- 明天的明天 永远的永远是什么意思
- 送给不珍惜我的人?是什么意思
- 我的心里只有你一个人,谁都代替不了你的位置。虽然在是什么意思
- 原来伤人的不是爱情,是回忆是什么意思
- 烟雨斜阳是什么意思
- 我走了,不再烦你了,对不起!无意中又打扰你了,以后是什么意思
- 远方的你还好吗?是什么意思
- 特么的这才是真正好的兄弟。是什么意思
- 希望這是妳最後一次不负我。是什么意思
- 春夏秋冬,生活一様過。是什么意思
- 给偶的内个她的一封信是什么意思
- 想你真好是什么意思
- 情书技巧之26字母情书大全是什么意思
- 挽回前女友还有必要吗
- 黑龙江婚姻家庭修复
- 情侣出轨被发现了怎么挽回
- 送对象八字情话短句
- 方城表白墙QQ
- 跟男神搭讪聊天
- 我的婆媳关系怎么维持
- 挽回前女友自我检讨书
- 婚礼纪加盟费用
- 挽回大嫂的婚姻
- 恋爱模拟人生剧情介绍攻略
- 怎么和英国女生搭讪聊天
- 出轨如何挽回双鱼座男友
- 恋爱不限时间游戏攻略女主
- 老婆两次出轨还能挽回吗
- 姓阙男宝宝属猴取名 推荐4个参考《论语》取名
- 姓邓男宝宝属马取名 推荐5个参考《诗经》取名
- 姓姬女宝宝属马取名 推荐6个参考《左传》取名
- 姓於男宝宝属猴取名 推荐10个参考《孟子》取名
- 姓逯男宝宝属鼠取名 推荐10个参考《国语》取名
- 姓鄂男宝宝属牛取名 推荐5个参考《庄子》取名
- 姓万俟男宝宝属马取名 推荐6个参考《韩非子》取名
- 姓司徒女宝宝属鸡取名 推荐9个参考《周易》取名
- 姓闻女宝宝属虎取名 推荐7个参考《论语》取名
- 姓沃男宝宝属狗取名 推荐3个参考《周易》取名
- 姓糜女宝宝属猪取名 推荐8个参考《韩非子》取名
- 姓於女宝宝属鸡取名 推荐3个参考《周易》取名
- 姓茅男宝宝属羊取名 推荐7个参考《论语》取名
- 姓乌男宝宝属鼠取名 推荐8个参考《韩非子》取名
- 姓米男宝宝属虎取名 推荐9个参考《左传》取名