标准差standard deviation

各变量值与其算术平均数的离差的平方的算术平均数的平方根，又称“均方差”，是统计学中最可靠、最合理、最常用的一种离中量数。样本标准差用S或SD表示，总体标准差用α表示。与平均差相比，它具有数学上易于处理的特点。平均差虽有其优点，但由于它采取绝对值的办法来消除离差的正负数，为了避免绝对值的缺陷，在统计学中就要采用标准差这一离中量数。也就是先将各项的离差数自乘，消去负号，平方以后再开平方根还原。由于各变量值与其算术平均数的差数平方之和为最小，所以标准差的计算一般皆以算术平均数为中心。同时，因标准差符合代数方法的运算，所以在统计研究中被广泛用来说明次数分配的离散趋势。标准差的计算方法：第一步，先求出各变量值与其算术平均数的离差，再把各项离差加以平方，并计算这些离差平方的算术平均数；第二步，将离差平方的算术平均数开方。从未分组材料求标准差，其公式为：

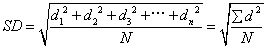
式中d₁, d₂, d₃, …d_n为一个量数系列中的每个量数与算术平均数的代数差。N为总次数。从分组材料求标准差，其计算公式为：

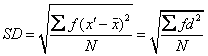
式中f为次数， 为平均数，x′为组中点，d为组中点与平均数之离差，N为总次数。