“数学期望”的意思、起源，数学期望是由谁提出的-心理学-情感百科-依恋情感网

网站首页情感咨询情感美文情感百科情感生活学习充电旧版美文

标题	数学期望
类别	心理学
释义	【数学期望】拼译：expectation 亦称“理论平均数”。概率论术语。随机变量重要特征数。用于说明随机变量取值的平均水平或集中趋势。若随机变量X的分布函数是F(x)，则E(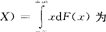X的数学期望。这里要求积分绝对收敛，否则X的数学期望不存在。若X是离散型随机变量，其分布列为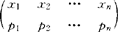，且级数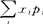_i绝对收敛，则将此级数和称为X的数学期望，]]；若级数不是绝对收敛，即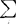｜x_i｜p_i发散时，则X的数学期望不存在。如，若X服从两点分布，其分布列为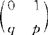，(q=1－p)，则E(X)=0q+1p=p。若X服从二项分布b(k；n，p)，则E(X)=np。若X是连续型随机变量，其密度函数是f(x)，且积分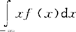绝对收敛，则X的数学期望存在，即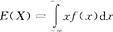。若X～N(μ，σ²)，则X的数学期望为E(X)=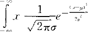dx=μ。
随便看	运动乐趣运动动机激励运动反应中间型运动反应感觉型运动反应时运动反应运动型运动反馈运动员心理衰竭运动员心理衰退运动员心理选材运动坚持性运动学习运动心理咨询运动心理定向运动心理应激运动心理战术手段运动心理治疗运动心理诊断运动心理障碍运动性失语症运动性幻觉运动情绪障碍运动意志障碍运动感知异常运动成就动机 staphylaceaes staphylagra staphylagrum staphyle Staphylea Staphylea bumalda staphylea bumalda dc. Staphyleaceae Staphylea forrestii Staphylea holocarpa staphylea holocarpa hemsl. staphyleas Staphylea shweliensis staphylectomia staphylectomy 古诗对诗人表达的情感有哪些是什么意思盼望情感语录短句是什么意思如何面对摩羯男的表白情书是什么意思发情感通知的文案简短句子是什么意思古装情感剧情的文案句子是什么意思成语励志情感文案语录是什么意思学生表达情感词语大全集是什么意思怪物学院美女情书是什么意思包含情感的散文名篇有哪些是什么意思天涯情感语录文案爱情是什么意思情书电影特效是什么意思情感暗恋文案大全是什么意思星空下情感文案是什么意思表达心情感悟的成语是什么意思打工人情感共鸣的句子是什么意思如何挽回婚姻,全方位挽回婚姻策略解析分手了怎么复合,揭秘挽回爱情的科学步骤与心理策略分手怎么复合,揭秘情感修复的六个关键阶段如何挽救婚姻危机,携手共筑幸福堡垒婚姻危机如何处理,识别、沟通与重建之道分手了怎么挽回男朋友,关键步骤与心理策略失恋了很难受怎么办,缓解痛苦，重拾生活光彩分手后还能挽回的10个征兆,这些征兆预示着复合的可能分手半年了怎么挽回前男友,分手半年后挽回前男友的攻略解析失恋了怎么办才能最快走出来,五大策略助你快速恢复男人在等你挽回的暗示,情感回温的信号与行动指南我跟女朋友分手了想挽回,重燃爱火，共筑未来教你挽回一个死心的人,挽回死心之人的五大策略解析如何挽回出轨的婚姻,出轨婚姻的挽回之道和男朋友分手了怎么挽回,挽回男友的实用攻略太阳巨蟹水星巨蟹的人怎么样太阳水星金星巨蟹座的区别水星巨蟹金星双子的人怎么样水星巨蟹座勤奋吗太阳巨蟹座水星天秤的明星有哪些怎么追到水星巨蟹座水星巨蟹座性格特点次限水星巨蟹座代表什么水星巨蟹座的性格表现水星巨蟹座水星巨蟹的男人靠谱吗水星巨蟹座精明吗三限水星巨蟹座是什么意思巨蟹座二宫水星代表什么水星巨蟹座的婚姻观水星巨蟹座适合的配偶

依恋情感网情感百科知识大全收录了49620条情感类百科知识词条，覆盖心理学、哲学、美学等领域，基本涵盖了日常生活中常见问题的详细解释，是情感生活的有利工具。