【贝叶斯判别】
拼译：Bayes discriminant
判别分析的一种方法。以平均误判损失最小为最优准则来建立判别规则，并以此对样品(被试)作出归属何个总体的判别分析。设有k个p维总体G1，G2，…，Gk，密度函数分别为fi(x)，各总体出现的先验概率为q1，q2，…，qk，记C(j|i)为实际来自Gi的样品误判到Gj产生的损失(i，j=1，2，…，k)，约定C(i|i)=0。又设D1，D2，…，Dk是根据判别规则产生的样本空间的一个划分，若样品x∈Di，则将x判归Gi(i=1，2，…，k)。在这些假设下，来自Gi的样品x被误判为Gj的概率为P(j|i)=|Djfi(x)dx，从而来自Gi的样品被误判的平均损失为L(Di)=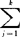
P(j|i)C(j|i)。于是总的平均误判损失为L(D1，D2，…，Dk)=
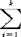qi
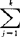P(j|i)C(j|i)。贝叶斯判别相当于选择样本空间的一个划分，使L(D1，D2，…，Dk)达到极小。记ht(x)=
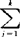qjfj(x)C(t|j)，t=1，2，…，k，贝叶斯判别的规则是：若x使得min｛ht(x)｝=hl(x)，则将x判归Gl。若误判损失都相同，则贝叶斯判别规则为：若x使得qlfl(x)＞qifi(x)(对所有的i)，则将x判归Gl。对于两个正态总体，若误判损失相同，先验概率也相同，贝叶斯判别与距离判别结果一致，判别函数和判别规则也一致。
- 德
- 德·摩根
- 德·摩根定理
- 德·曼
- 德乌斯图亚
- 德力之争
- 德勒泽
- 德国
- 德国古典哲学
- 德国浪漫派美学
- 德奥佛拉斯多斯
- 德尔图良
- 德布罗意
- 德性之知
- 德拉-沃尔佩
- 德操
- 德日进
- 德治
- 德波林
- 德波林学派
- 德盛文缛
- 德索
- 德索尔
- 德苏瓦尔
- 德莱登
- Massachusettsan
- Massachusettsans
- Massachusetts Association of Hazardous Material Technicians
- massachusetts b.
- Massachusetts ballot
- Massachusetts Bay
- massachusetts bay colonies
- Massachusetts Bay Colony
- Massachusetts Bay Community College
- Massachusetts Bay Company
- massachusetts bays
- Massachusetts College of Art
- Massachusetts College of Optometry
- Massachusetts Coll of Pharmacy and Allied Health
- Massachusetts, Commonwealth of
- 蜀相表达诗人什么情感是什么意思
- 匿名情书在线观看是什么意思
- 借助他人的文章来表达自己的情感是什么意思
- 情书loveletter香水是什么意思
- 情书徐静蕾1999是什么意思
- 相爱情感语录表情包是什么意思
- 表达情感的高级句式是什么意思
- 婚礼爸爸妈妈情感文案是什么意思
- 猫在地上打滚表达什么情感是什么意思
- 情感诗词文案高级句子简短是什么意思
- 拉萨古城表达了怎样的情感是什么意思
- 情感语录文案名人是什么意思
- 情感类文案用什么名字好听是什么意思
- 张艺谋最好看的情书电影是什么意思
- 情感散文甜蜜文案是什么意思
- 社交软件女生主动搭讪聊天
- bigbang成员感情
- 怎么挽回拉黑的处女座男友
- 潮汐恋爱游戏攻略小说
- 分手挽回女友礼物文案搞笑
- 最搞笑龅牙仔相亲记
- 女生向男生表白文案圣诞
- 贵州贞丰苗族婚礼视频
- 男孩子如何搭讪女孩子聊天
- 亲吻对方私密代表什么感情
- 情感挽回的博主推荐
- 梦见表白自己什么意思
- 婚礼现场喜欢唱的歌
- 福州夫妻情感挽回在线咨询
- 北京小伙婚礼感人讲话视频
- 夏季高温养生秘籍：5种清热解毒的美味佳肴
- 夏季女性养生必备:5种营养丰富的食物推荐
- 夏季养生必喝的5款中医养生汤
- 夏季养生必喝的5款清热解毒汤品
- 夏季女性养生茶的最佳搭配
- 夏季养生壶煲茶水的5大秘诀
- 夏季养生必备:5种最佳煮水饮品推荐
- 夏季养生煮什么最好?5种养生壶煮饮品推荐
- 夏季养生必喝的5款养生茶
- 夏季养生16个实用小贴士
- 夏季养生必备:5大实用养生技巧助你轻松度过炎热夏日
- 夏季产后妈妈必备的5款养生汤
- 夏季养生必喝的5款养生汤品
- 夏季钓鱼的养生之道
- 夏季养生汤品推荐 - 广州地区流行的几款养生汤