【二项分布】
拼译:binomial distribution
离散型随机变量概率分布的一种。在n重贝努里试验中,若事件A在n次试验中出现的次数X的概率分布是:b(k;n,p)=P(X=k)=( )pkqn-k,(k=0,1,2,…,n),式中p是A在一次试验中出现的概率(0<p<1),q=1-p,则称X服从二项分布。根据离散型随机变量平均数(即数学期望)的定义公式E(X)=
)pkqn-k,(k=0,1,2,…,n),式中p是A在一次试验中出现的概率(0<p<1),q=1-p,则称X服从二项分布。根据离散型随机变量平均数(即数学期望)的定义公式E(X)=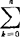 k·
k·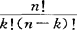 pk·qn-k=np
pk·qn-k=np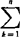 (
(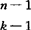 )pk-1qn-k=np(p+q)n-1=np,可求出二项分布随机度量X的平均数为np。可用DX=E(X2)-(EX)2公式和E(X2)=
)pk-1qn-k=np(p+q)n-1=np,可求出二项分布随机度量X的平均数为np。可用DX=E(X2)-(EX)2公式和E(X2)=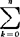 k2(
k2( )pkqn-k=npq+n2p2计算出二项分布随机变量X的方差DX=npq+n2p2-(np)2=npq,其标准差为
)pkqn-k=npq+n2p2计算出二项分布随机变量X的方差DX=npq+n2p2-(np)2=npq,其标准差为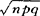 。
。
- 衰老性记忆下降
- 衰老性退缩行为
- 被动人模型
- 被动性性角色
- 被动攻击型人格障碍
- 被动注意
- 被动睡眠说
- 被控制感
- 被洞悉感
- 被试变量
- 裁判员偏袒宣判模拟
- 裂脑综合征
- 西南部诸文化的心理学类型
- 西奥菲斯塔性格说
- 西藏心灵治疗
- 观众心理
- 观众效应
- 观众模拟
- 观察力的发展
- 观察学习
- 观察学习理论
- 观察法
- 观察视野
- 观念飘忽
- 规范失调
- Neutral position
- neutral position of brush
- neutral positon
- neutral potassium arsenite
- neutral potassium bromide
- neutral potassium iodide
- neutral potassium iodide method
- neutral potato
- neutral potential
- neutral power
- neutral premetallized dyes
- neutral pressure
- neutral pressure level
- neutral pressure plane
- neutral pressure process
- 爱的很寂寞情感语录是什么意思
- 杯杯酒中情感语录是什么意思
- 情书日语版简介是什么意思
- 表达难过的情感是什么意思
- 情感语录那么累是什么意思
- 短小情感书单文案怎么写是什么意思
- 国庆快乐的情感散文诗是什么意思
- 教师节语录情感句子是什么意思
- 狡猾的情感好句子是什么意思
- 用药物写情书是什么意思
- 情感散文题目经典语录是什么意思
- 感叹号表达了作者怎样的情感是什么意思
- 情书就一个字概括是什么意思
- 我和你的歌表达什么情感是什么意思
- 表达情感未产生共鸣的诗句是什么意思
- 老公出轨的婚姻还有救吗?老公出轨了怎么挽回?
- 老公出轨了怎么挽回?有效挽回家庭的3个方法
- 面对老公出轨先别慌,女人想挽救家可以这样做!
- 老公出轨了如何挽回家庭?
- 老公出轨怎么办?解决老公出轨的方法
- 夫妻感情不和老公出轨怎么办?
- 男人出轨了还会回头吗?老公出轨怎么办?
- 不幸的婚姻是什么导致的?
- 使婚姻生活幸福快乐方式
- 为什么别人的婚姻很幸福,你的却一塌糊涂?
- 如何经营婚姻才能充满激情呢?
- 婚姻生活不顺遂,一定要多考虑这个方面!
- 运营幸福美满婚姻的方法
- 纠正不正确的夫妻状态,婚姻生活才会圆满
- 夫妻如何把握美满婚姻沟通技巧
- 茉莉花果实的多重功效:从美容养颜到健康调理
- 白蒿的神奇功效:从祛湿到抗菌,这种野草竟然如此神奇
- 搓手的好处:提高免疫力、改善血液循环、缓解疲劳
- 天麻的多重功效:从改善睡眠到增强免疫力
- 壁虎的神奇功效:从生吃到药用,这些你都知道吗?
- 核桃的营养价值与健康功效
- 黄连的神奇功效:从清热解毒到调理肠胃
- 碘元素的重要功能及其在人体中的作用
- 野玉米的营养价值与健康功效
- 吃麦冬的6大功效与作用,你了解多少?
- 椿皮的神奇功效:从养生到医疗的多重价值
- 藏茶的神奇功效:提升健康、改善生活
- 甜叶子的神奇功效:从减肥到调节血糖,这种植物有着意想不到的用途
- 萝卜的营养价值与健康功效
- 水苏糖的神奇功效:改善睡眠、调节血糖、抗氧化