“二元正态分布”的意思、起源，二元正态分布是由谁提出的-心理学-情感百科-依恋情感网

网站首页情感咨询情感美文情感百科情感生活学习充电旧版美文

标题	二元正态分布
类别	心理学
释义	【二元正态分布】拼译：bivariate normal distribution 一译“双变量正态分布”。正态分布的一种。一元正态分布在二元情形下的推广。若(X₁，X₂)是二维随机向量，其联合密度函数为f(x₁，x₂)=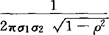·exp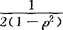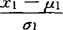｛－［()²－2_ρ(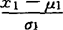)()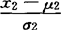+()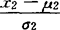²］｝，(对一切－∞＜x₁＜+∞，－∞＜x₂＜+∞成立)，式中μ₁，μ₂，σ₁，σ₂，ρ是分布的五个参数，σ₁＞0，σ₂＞0，｜ρ｜＜1，则称(X₁，X₂)服从二元正态分布。二元正态分布的二个边际分布是两个一元正态分布，即f₁(x₁)=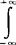f(x₁，x₂)dx₂=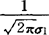e^－(x1－μ1)^2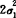／，(对一切－∞＜x₁＜+∞)，f₂(x₂)=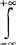f(x₁，x₂)dx₁=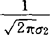e^－(x₂^－μ2)²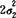／，(对一切－∞＜x₂＜+∞)，即X₁～N(μ₁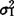，)，X₂～N(μ₂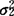，)。二元正态分布情况下，两个变量的独立性与相关性是等价的(注意，一般情况下，此结论未必成立)。因为X₁与X₂之间的相关系数ρ=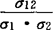，式中σ₁₂是X₁与X₂之间的协方差，即σ₁₂=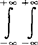(x₁－μ₁)(x₂－μ₂)f(x₁，x₂)dx₁dx₂。当ρ=0与σ₁₂=0是等价的，再由(X₁，X₂)的联合密度函数f(x₁，x₂)看出，若ρ=0，推出f(x₁，x₂)=f₁(x₁)·f₂(x₂)，即X₁与X₂相互独立，反之亦成立。
随便看	人机系统人格人格动力学人格心理学人格性别差异人格效应人格整合人格整合不良人格社会化人格解体人格适应人格障碍人物资料法人生发展课题理论人电催眠法人痾人的传递函数人的传通人的判据人的可靠性人的因素评价人的模拟人的自我沟通人类信息符号系统人类因素工程 mass fusion splicing machine mass gaining star mass game mass gastric survey equipment Mass gathering mass generation curve mass genetic dose mass GI survey massgoers mass goods Mass grave Mass graves mass growth mass halllucination Mass hallucination 情感拍照文案搞笑句子大全是什么意思哥哥情感语录头像女高级是什么意思饮酒一诗表达了作者怎样的情感是什么意思高中语文散文情感教学设计是什么意思雨中情情感散文是什么意思花样梁祝情感音乐文案图片是什么意思故事元日表达了什么情感是什么意思肖战情感语录视频是什么意思情书平淡是什么意思幸福情感高级文案简短句子是什么意思插花吟表达的情感是什么意思疫情情感励志文案图片大全是什么意思魂牵梦绕的情书是什么意思影史情书地位是什么意思春节的情感散文是什么意思离婚带孩子的女人怎么办老公不愿意和我沟通是怎么回事想结婚又怕离婚怎么办错误的婚姻要不要继续感觉自己什么都没有了怎么办老婆不付出还经常抱怨，我很烦怎么办老婆嫌我挣钱少，对我冷淡怎么办老婆说对我没感情了，却一直拖着不分开精神世界不同的两个人该怎么办最近患相亲恐惧症，电话恐惧症怎么办和老婆总是吵架，她要离婚怎么办已婚女人能接受单身男的邀请吗老婆说我不够关心她，我不想跟她分开女方做了类似背叛的事情，要怎么修复关系幸福的婚姻大都相似，不幸的婚姻各有不同月经前吃这些食物,让你轻松度过经期牙龈出血时这些食物可以帮助止血和修复如何补充钾元素?钾元素的食物来源及摄入建议如何缓解腹胀?这些食物可以帮你轻松解决小肠出血的饮食调理方法肾虚症状及食疗调理方法心火旺盛?这些食物可以帮你降火解毒喉息肉患者饮食指南:合理饮食助力康复孕期腿部疼痛的缓解方法及食疗建议血栓形成的常见症状及预防饮食建议甲状腺亢进饮食指南:合理饮食助你调理症状女性养胃必吃的5种食物肌无力患者的饮食指南:营养丰富的食物助力康复夏季降暑必备!这些清凉美味的食物你一定要知道色素减退的原因及食疗方案

依恋情感网情感百科知识大全收录了49620条情感类百科知识词条，覆盖心理学、哲学、美学等领域，基本涵盖了日常生活中常见问题的详细解释，是情感生活的有利工具。