【X2分布】
拼译：chi square distribution
一译“卡方分布”。数理统计分布的一种。赫尔梅特1875年在研究正态总体样本方差时发现。若ξ是连续型随机变量，其密度函数fξ(x)=
，则称ξ服从自由度为n的X2分布。X2分布的密度函数fξ(x)的图形(如下图)。若ξ1，ξ2，…，ξn是相互独立的标准正态随机变量，则它们的平方和
=
+
+…+
服从自由度n的X2分布，并记为
～X2(n)。X2分布分中心X2分布和非中心X2分布，它们在正态线性模型误差方差的估计理论、正态总体方差的检验、正态变量的二次型理论中均有重要作用。
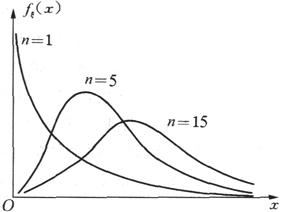
不同自由度的X2分布密度函数曲线
- 总分常模
- 总变异
- 总合作用
- 总平方和
- 总结性测验
- 总结性评量
- 总觉
- 总量作用
- 恋女情结
- 恋子情结
- 恋尸取向
- 恋尸性格
- 恋母情结
- 恋爱
- 恋爱从众心理
- 恋父情结
- 恋物癖
- 恋生取向
- 恋生性格
- 恐怖性格
- 恐怖症
- 恐惧
- 恐惧性神经症
- 恐惧疗法
- 恐惧症
- burst transfer rate
- Burst transmission
- bursttransmission
- burst trap
- burst trapping code
- burst type error
- burst tyre
- burst up
- burst upon
- burst upon the view
- burst wave
- burst wave form
- burst waveform
- burst width
- burst with
- 山水散文情感有哪些是什么意思
- 小情书过年好是什么意思
- 写散文情感文的订阅号是什么意思
- 小豆言情书城是什么意思
- 表达世间情感的散文是什么意思
- 泰国小孩表达自己情感的歌是什么意思
- 长相思主要表达情感吗为什么是什么意思
- 枫叶情感文案创作思路分析是什么意思
- 蚂蚁森林情书是什么意思
- 怎样将情感融入表达中是什么意思
- 情感分手日记短句子伤感是什么意思
- 情感生活文案婆媳是什么意思
- 情感文案句子大全伤感图片是什么意思
- 情感里掺杂了虚荣心的句子是什么意思
- 情感散文回归短篇是什么意思
- 小三怎么做让男人主动和原配离婚的？原配如何手撕高段位小三？
- 520送老婆祝福话语，520祝福文案
- 情感语录丨在爱情的花海中，找到了一朵属于我们的花。
- 情感语录丨在你身边，时间悄悄溜走，留下的是深深的爱和美好的回忆。
- 失恋后感慨的句子适合发说说的文案
- 儿子失恋了有点抑郁怎么办？家长该做些什么呢？
- 失恋后抑郁了怎么办？尝试这10招打败失恋后抑郁！
- 怎么挽回一段快要失去的感情？挽回恋人有效的3个方法。
- 老公和小三还联系,怎么应对？原配的聪明做法
- 怎样让老公和小三反目？学会这些技巧轻松分离小三
- 男人会为哪种小三离婚？她们究竟有何魔力让男人忍不住离婚？
- 男人会为哪种小三离婚？男人在什么情况下会为小三离婚？
- 情感语录丨怎么挽回一段快要失去的感情短句
- 情感语录丨失约了该如何高情商的回答句子
- 老婆对老公失望了怎么挽回,幽默挽回老婆的话
- 胃阴虚吃什么食物好：滋阴养胃食物推荐与调理方案
- 肺气肿吃什么食物好？最佳饮食方案全攻略
- 心衰病人吃什么食物好：专业营养师推荐食谱
- 多囊卵巢吃什么食物好,症状改善-完整饮食指南
- 胃反酸吃什么食物好？饮食调理方案与科学选择指南
- 肺结节吃什么食物好：营养学视角的饮食管理策略
- 肚子胀吃什么食物好？科学饮食缓解胃胀气全攻略
- 来月经吃什么食物好,调理经期不适的饮食策略
- 中暑吃什么食物好？防暑降温饮食指南与营养补充方案
- 风湿吃什么食物好,抗炎营养方案-膳食调理全指南
- 大便不成形吃什么食物好-调理肠胃饮食指南
- 对眼睛好的食物有哪些？专家解析护眼饮食方案
- 反胃吃什么食物好,肠胃不适饮食指南-科学调理方案解析
- 降血脂食物推荐清单，科学配餐指南全解析
- 脾阳虚吃什么食物好？温补食谱与饮食禁忌全解析