加权算术平均数weighted arithmeticmean

以各种变量在总体或样本中出现的次数或所占的比重作为权数计算的算术平均数。用Mw表示。它也是反映集中趋势的一种量数。把变量值整理成单项数列时，以各种变量值的频数作为权数计算加权算术平均数，其公式为：

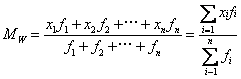
式中x₁,x₂…x_n代表各个变量，f1,f2…fn代表x₁,x₂，…x_n的权数。上式可用于已知同类数据求总平均数，或者用于已知若干个小组平均数求总平均数。加权平均数的大小，不仅决定于总体或样本各单位的标志值，也决定于各标志值的权数。权数大的标志值对平均数的影响就大，反之则相应地小些。在组距分配数列中，加权平均数的计算，要以各个组平均数(即上式的x₁,x₂，…x_n为各组平均数)乘以相应的权数。在缺少组平均数资料的情况下，则用各个组距的组中值代表各组的平均数(此时上式中的x₁,x₂…x_n为各组组中值)。