【费希尔Z检验】
拼译：Fisher’s Z test
相关系数显著性检验方法的一种。适合以下两种情况：(1)H0：ρ=ρ0(ρ0≠0)；H1：ρ≠ρ0，即总体相关系数ρ与一已知非零数ρ0的差异是否显著；(2)H0：ρ1=ρ2；H1：ρ1≠ρ2，即两个总体相关系数是否相等的检验。在检验前，要先将样本相关系数r转换为费希尔Zr，即按Zr=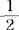
ln(
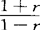)。公式对r作变换，以解决相关系数不可加问题。然后才构造检验统计量Z对统计假设H0：ρ=ρ0(ρ0≠0)，则Z=
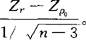。式中Zr与Zρ分别为r与o的费希尔Zr值，在H0成立时，Z服从正态分布。对于统计假设H0：ρ1=ρ2，统计量是Z=
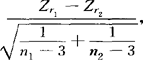，其中r1与r2为两独立总体中抽得的样本相关系数，n1与n2为它们的样本大小。Z在H0成立时呈正态分布。以上检验均为双侧检验。
- 《乐》
- 《乐书》
- 《乐律全书》
- 《乐经》
- 《乐记》
- 《乐论》
- 《乙丙之际箸议》
- 《九章集》
- 《习学记言》
- 《习学记言序目》
- 《乡村建设理论》
- 《书》
- 《书写语言学》
- 《书古微》
- 《书序》
- 《书断》
- 《书经》
- 《书谱》
- 《二十一世纪议程》
- 《二十世纪的怪物——帝国主义》
- 《二十世纪西方伦理学》
- 《二十二年来之中国哲学思潮》
- 《二十四诗品》
- 《二曲集》
- 《二林居集》
- gambusia
- Gambusia affinis
- gambusia affiniss
- Gambuta, Gunung
- Gambôa
- Gambēla
- Gambēla Hizboch
- Gambēla National Park
- gamc
- gamco
- Game 39
- gameable
- game act
- game acts
- game against nature
- 人生语录经典情感短句是什么意思
- 情书第9是什么意思
- 情感散文诗优美句子摘抄是什么意思
- 情感简短散文诗句长篇是什么意思
- 情感语录大全免费的是什么意思
- 婚姻语录情感视频伤感版是什么意思
- 名人说放下的情感语录是什么意思
- 人生情感语录800句是什么意思
- 水王子的情书是什么意思
- 许你在见钟情书评是什么意思
- 婚介情感语录文案简短是什么意思
- 大学爱情语录情感动漫是什么意思
- 农村大集的情感语录是什么意思
- 玩女娲的情感语录是什么意思
- 情书交响是什么意思
- 官宣恋爱攻略知乎小说完结
- 怎样挽回出轨天蝎女的
- 男友想挽回我要怎么办
- 哈里王婚礼直播
- 婚礼西服颜色
- 如何搭讪学霸帅哥聊天呢
- 情话最好听
- 长春婚姻挽回机构
- 挽回情感语录婚姻上的冲突
- 法定感情破裂
- 游戏恋爱攻略的攻略
- 手工陶艺情话
- 不去参加婚礼的理由
- 跟女生表白之后的聊天话题
- 请婚姻专家挽回效果怎么样
- 滴滴打车是你购买某些商品的最佳选择
- 武汉最适合练车的地方推荐
- 如何选择适合的防冰雹车罩品牌
- 如何选择适合的车衣
- 如何选择上下爬楼梯车？五大品牌推荐
- 如何选择交通工具从南通回苏州最合适
- 选择小牛电瓶车的最佳电瓶
- 车钥匙保护套推荐：选购指南与品牌推荐
- 选择车用地垫的最佳材质有哪些？
- 大众速腾车机选择指南：为你推荐最适合的车机系统
- 豪华汽车的内饰和音响品质一览
- 2024年四款热门小型电动车推荐
- 为什么CRV比国产车更优秀？
- 2024年东北电动车市场上哪种电池最适合？
- 如何选择适合拖挂房车的前车