“熵”的意思、起源，熵是由谁提出的-心理学-情感百科-依恋情感网

网站首页情感咨询情感美文情感百科情感生活学习充电旧版美文

标题	熵
类别	心理学
释义	【熵】拼译：entropy 描述一个事件不确定性程度的量度。美国数学家申农提出。设X是离散型随机变量，取值是a₁，a₂，…，a_k，…(至多可列个)，且P_r(X=a_i)=p_i(i=1，2，…)，则称“－∑p_ilnp_i”为X的熵，并记为H(X)，即H(X)=－∑p_ilnp_i(注意，上面式中规定当p_i=0时，0·1n0=0)。对于连续型随机变量X，若X～p(x)，且积分“－∫p(x)lnp(x)dx”有意义，则称为p(x)(或X)的熵。如参数空间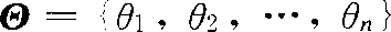，若p(θ_k)=1，p(θ_i)=0(当i≠k时)。即θ以概率1取θ_k是肯定的，于是我们求得墒是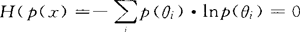。这是不确定性最小的极端情形。若p(θ_i)=1／n，(i=1，2，…，n)于是有H(p(x)=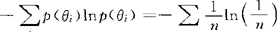=lnn。可见，均匀分布的熵最大。
随便看	force platform foreign language learning aptitude forensic psychiatry forensic psychiatry, judical psychiatry forensic psychology forests in urban area forgetting forgetting curve form form adaptation formal communication formal feeling formal group formalism formalization formal-operational stage formal organization formal sense of fine arts formal thinking formal training theory of learning form analysis formant formation of testimony formative evaluation formative test Win 18320 WIN 2005 WIN 22005 WIN32 WIN 32729 Win32 API Windows win32 driver model Win32s Win32 Spooler win32 subset Win351972 Win 35197 2 Win 38020 Win40680 Win 40680 情感语录无常是什么意思情感散文集精选是什么意思成长情感类散文名篇大全是什么意思仿写勿勿表达情感的句子是什么意思情感语录迷人的她是什么意思描写夏天情感文案句子简短是什么意思散文阅读把握主旨情感是什么意思登飞来峰这首诗表达的情感是什么意思关于情感表达的演讲稿是什么意思根据济慈的爱情感想散文是什么意思梧桐雨的情感表达是什么意思情感剧情带货文案是什么意思把握散文情感的方法是什么意思情感语录经典短句慢慢是什么意思中国人的情感表达调查研究是什么意思酒店婚礼场景挽回男友高手婚姻家庭矛盾纠纷调解制度农村国宝表白的视频大全男人对感情失去安全感恋爱助手脱单技巧攻略大全婆媳关系十几年了游戏恋爱生宝宝攻略大全前男友生病了想挽回他了错过之后还能否挽回婚姻婚姻挽回中如何调节心态做生意的女人没有感情吗鲁西南婚礼杨幂婚礼伴娘情话刀鞘金星白羊座女生口才怎么样金星白羊座感情观太阳天秤金星白羊座金星白羊座内心需求金星白羊座金星天秤的男生靠谱吗金星白羊上升金牛的男人靠谱吗给金星白羊座的建议金星十宫白羊座代表什么金星白羊座女生魅力怎么样太阳金星星座白羊座的男人靠谱吗金星白羊座的性格金星白羊座一宫代表什么金星白羊座与妈妈关系怎么样金星狮子上升白羊座的男人靠谱吗金星白羊座男智商怎么样

依恋情感网情感百科知识大全收录了49620条情感类百科知识词条，覆盖心理学、哲学、美学等领域，基本涵盖了日常生活中常见问题的详细解释，是情感生活的有利工具。