【正态总体方差假设检验】
拼译:test of hypothese on variance of normal distribution
假设检验的一种。对正态总体方差进行的统计检验。主要有以下几种情况。(1)一个总体情形下,正态总体方差用X2检验。设总体X~N(μ0,σ2),若μ=μ0已知,待检验的假设是H0:σ2=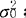 ;H1:σ2≠
;H1:σ2≠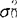 。使用的检验统计量X2=
。使用的检验统计量X2=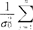 (Xi-μ0)2在H0成立时服从自由度为n的X2分布。由给定的显著水平α,查X2分布数值表得上、下侧
(Xi-μ0)2在H0成立时服从自由度为n的X2分布。由给定的显著水平α,查X2分布数值表得上、下侧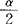 分位点
分位点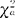 /2与
/2与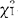 -α/2,满足P{X2≤
-α/2,满足P{X2≤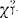 -α/2}=P{X2≥
-α/2}=P{X2≥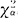 /2}=
/2}=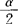 。由样本算出X2的观测值
。由样本算出X2的观测值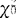 。拒绝H0的条件是X2≤
。拒绝H0的条件是X2≤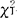 -α/2或X2≥
-α/2或X2≥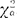 /2。若总体均值μ未知,所使用的检验统计量不同,其余部分与上面讨论相同。这时采用的统计量是X2=
/2。若总体均值μ未知,所使用的检验统计量不同,其余部分与上面讨论相同。这时采用的统计量是X2=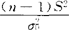 =
=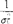 ·
·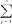 (Xj-
(Xj-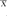 )2。在H0成立时它服从自由度为n-1的X2分布。(2)两个总体情形下,正态总体方差用F检验。设两个相互独立的总体X1与X2,X1~N(μ1,
)2。在H0成立时它服从自由度为n-1的X2分布。(2)两个总体情形下,正态总体方差用F检验。设两个相互独立的总体X1与X2,X1~N(μ1,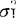 ),X2~N(μ2,
),X2~N(μ2,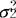 )。所有参数都未知,待检验的假设是H0:
)。所有参数都未知,待检验的假设是H0: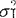 =
=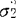 ;H1:
;H1: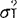 ≠
≠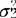 。从X1抽取样本X11,X12,…,X1n;从X2抽取样本X21,X22,…,X2n2。检验H0的统计量是F=
。从X1抽取样本X11,X12,…,X1n;从X2抽取样本X21,X22,…,X2n2。检验H0的统计量是F=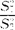 =
= 。在H0成立时,F服从自由度为(n1-1,n2-1)的F分布。由给定的α查F分布数值表得上、下侧α/2分位点Fα/2和F1-α/2,它们满足P:F≥F。/2}=P{F<F1-α/2}=
。在H0成立时,F服从自由度为(n1-1,n2-1)的F分布。由给定的α查F分布数值表得上、下侧α/2分位点Fα/2和F1-α/2,它们满足P:F≥F。/2}=P{F<F1-α/2}=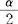 。若F的观测值F0≥Fα/2或F0≤F1-α/2,则拒绝H0;否则,接受H0。(3)k(k>2)个总体情形下,用巴特利特检验(方差齐性检验的一种)。设有k个相互独立且服从正态分布的总体X1,X2,…,Xk。现要检验它们的方差是否相等:H0:
。若F的观测值F0≥Fα/2或F0≤F1-α/2,则拒绝H0;否则,接受H0。(3)k(k>2)个总体情形下,用巴特利特检验(方差齐性检验的一种)。设有k个相互独立且服从正态分布的总体X1,X2,…,Xk。现要检验它们的方差是否相等:H0: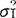 =
=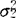 =…=
=…=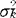 ,H1:H0不真。记Xij(i=1,2,…,k;j=1,2,…,ni)为k个独立样本。样本方差
,H1:H0不真。记Xij(i=1,2,…,k;j=1,2,…,ni)为k个独立样本。样本方差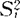 =
=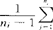 (Xij-
(Xij-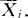 )2。检验H0的统计量是X2=2.3026[log10S2
)2。检验H0的统计量是X2=2.3026[log10S2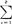 (ni-1)-
(ni-1)-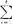 (ni1)log10
(ni1)log10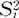 ]·
]·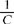 。在H0成立时,它趋近于自由度为k-1的X2分布。当X2≥
。在H0成立时,它趋近于自由度为k-1的X2分布。当X2≥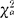 :(k-1)时,拒绝H0。其中
:(k-1)时,拒绝H0。其中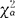 :(k-1)是X2分布的右侧α分位点:P{X2>
:(k-1)是X2分布的右侧α分位点:P{X2>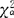 :(k-1)}=α。式中C与S2含义如下:C=1+
:(k-1)}=α。式中C与S2含义如下:C=1+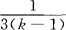 [
[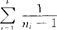 -
-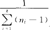 ],S2=
],S2=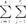 (Xij-
(Xij-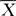 i)/
i)/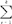 (ni-1)。
(ni-1)。
- irritable infant
- irrumation
- I-self
- isokinetric contraction
- isolated star
- isolating mechanism
- isolation
- isolation effect
- isolation experiment
- isometric contraction
- isomorphism
- isosensitivity curve
- isotonic constriction
- itch
- IT Children Scale
- item analysis
- item bank
- item characteristic curve
- item characteristic function
- item difficulty
- item difficulty index
- item discrimination
- item discrimination index
- item information function
- item-marking technique
- transaction execution flow
- transaction exposure
- transaction facility
- transaction failure
- Transaction fee
- Transaction fees
- transaction file
- transaction files
- transaction flow
- transaction flow language
- transaction flow manager
- transaction for account
- transaction for forward delivery
- transaction formatting routines
- transaction for money
- 梳子幼儿诗主要表达什么情感是什么意思
- 江南美景情感语录短句摘抄是什么意思
- 迎新春抗疫情书签是什么意思
- 情感不顺利的文案句子短句是什么意思
- 情感扎心文案醉酒句子伤感是什么意思
- 药老情感语录是什么意思
- 情感文案馆生日文案是什么意思
- 台阶的结尾表达的情感语录是什么意思
- 情书超可爱是什么意思
- 原神胡桃情感语录是什么意思
- 治愈系情感短剧文案素材是什么意思
- 表达爱国情感的边塞诗歌是什么意思
- 文案情感共鸣每日推荐是什么意思
- 情感的陪护总结文案是什么意思
- 优美的情感语录散文诗句是什么意思
- 心理学如何挽回出轨老公
- 老发现老公出轨怎么挽回
- 要和老公离婚了该怎么挽回
- 老公出轨女人应怎么挽回
- 跟老公冷战说分手怎么挽回
- 女人对老公失望了怎么挽回
- 和老公没有感情怎么挽回
- 老公说我要离婚怎么挽回
- 老公厌烦我我该如何挽回
- 经常对老公发脾气怎么挽回
- 老公不顾家该怎么挽回婚姻
- 女人背叛后挽回老公的方法
- 女人外遇怎么挽回老公的心
- 老公脾气大怎么挽回他的
- 要离婚怎么挽回老公的感情
- 月亮射手座月亮狮子座合适吗
- 摩羯座月亮太阳星座的区别
- 太阳摩羯座上升射手的人怎么样
- 月亮摩羯座可悲之处
- 月亮落在摩羯座男生人怎么样
- 太阳摩羯座月亮摩羯男性格怎么样
- 月亮白羊月亮摩羯合适吗
- 太阳摩羯月亮白羊的男人靠谱吗
- 太阳射手座月亮射手座上升射手座的人怎么样
- 月亮摩羯座是落陷吗
- 月亮摩羯座与月亮摩羯座合适吗
- 月亮巨蟹月亮摩羯合适吗
- 月亮摩羯座和什么搭配
- 上升摩羯座月亮双鱼的人怎么样
- 月亮摩羯座清醒吗