【分布函数】
拼译：distribution function
亦称“累积分布函数”。概率论术语。设X为随机变量，则F(x)=P(X≤x)(－∞＜x＜+∞)为X的分布函数。有离散型分布函数和连续型分布函数两种。分布函数F(x)的函数值等于随机变量X取值在(－∞．x］上的随机事件的概率。分布函数F(x)具有如下性质：(1)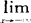
F(x)=0，或写成F(－∞)=0：(2)
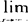F(x)=1，或写成F(+∞)=1；(3)右连续性：对任意－∞＜a＜+∞，有
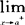F(x)=F(a)；(4)单调性：若x1＜x2，则F(x1)≤F(x2)，即F(x)是个非递减函数(注：按我们这里定义的F(x))；(5)若(a＜x≤b)是个随机事件，则F(a＜x≤b)=F(b)－F(a)。分布函数是个分析性质良好的函数，便于数学处理，使许多概率问题转化为函数的运算。设离散型随机变量所有可能取值为xi(i=1．2，…)，其概率P(xi)=Pi，Pi满足Pi≥0和
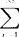Pi=1，由上面的分布即得分布函数F(x)=
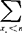Pi。连续型随机变量的分布函数为F(x)=
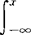φ(x)dx，其中φ(x)是概率密度函数。参见“概率密度函数”。
- James-Lange theory
- James-Lange theory of emotion
- James Mark Baldwin
- James Mckeen Cattell, Raymond Bernard Cattell
- James Mill, John Stuart Mill
- James Olds
- James Rowland Angell
- James Ward
- Jan Evangelista Purkinjé
- Japanese Academic Conference Liaison Council for Psychological Research
- Japanese illusion
- Japanese Psychology Association
- Jastrow illusion
- Jay Haley
- J coefficient
- jealous offense
- jealousy
- Jean-Baptiste de Monet Lamarck
- Jean Henri Fabre
- Jean Jacques Rousseau
- Jean Marie Faverhe
- Jean-Martin Charcot
- Jean Maurice Lahy
- Jean Paul Sartre
- Jean Piaget
- parasitic granuloma
- parasitic habit
- parasitic hematochezia
- parasitic hemoptysis
- parasitic hepatic cirrhosis
- parasitic host
- parasitic hymenoptera
- parasitic hypothesis
- parasiticidal
- parasiticidal therapy
- parasiticide
- parasitic image
- parasiticin
- Parasitic inductance
- Parasitic infection
- 抖音剪辑情感语录怎么赚钱是什么意思
- 情感散文怎么找到文案素材是什么意思
- 信封情书项链推荐是什么意思
- 女人情感散文诗是什么意思
- 好漂亮的情书是什么意思
- 情感案例语录摘抄经典是什么意思
- 秋天搞笑情书是什么意思
- 庄子散文蕴含什么情感是什么意思
- 释怀失败情感语录视频是什么意思
- qq飞车交往情书是什么意思
- 散文台词情感分析方法总结是什么意思
- 墨陌的情感语录是什么意思
- 爱情感动散文名篇大全集是什么意思
- 带有情感的散文600字是什么意思
- 情感语录收徒要求高是什么意思
- 一段感情太累该放手吗
- 吉永老师约会小技巧女生
- 异地女友分手2次怎么挽回
- 挽回男友有趣对话
- 分手情感挽回文案长句图片
- 婚礼拍照构图
- 约会后聊天技巧女生不理你
- 前任男友怎么去挽回我的话
- 男车主与女乘客搭讪聊天
- 怎么挽回出轨男友
- 分手20天后挽回情感
- 约会技巧日本综艺
- 相亲男朋友出轨了怎么挽回
- 挽回婚姻的本质有哪些呢
- 挽回前男友去他公司看看
- 安徽秋季养生汤大全｜哪些品牌值得品尝
- 秋季养生知识大揭秘，让你健康过秋
- 秋季养生进补的药汤有哪些？ | 精选5种药材药汤，助您进补秋季
- 秋季养生指南：健康生活的秘诀
- 秋季养生时尚：探索高端养生菜品 Top 5
- 冬秋季养生饮品大揭秘！了解这些饮品，助你迎接寒冷的季节
- 秋季热灸养生，你知道吗？| 热灸的健康益处和方法
- 秋季萝卜养生：多种吃法带给你健康好处
- 秋季养生汤配菜有哪些
- 秋天养生食疗：享受健康的美食
- 秋季养生汤的10大品牌推荐，珠海地区专供
- 秋季养生营养粥排行榜，推荐几个知名品牌
- 秋季养生菜谱：为你推荐9种适宜秋季食用的蔬菜
- 男人迎接秋季时，如何保持健康和养生
- 秋季养生必备！中医推荐的5款营养汤