“多值逻辑”的意思、起源，多值逻辑是由谁提出的-哲学-情感百科-依恋情感网

网站首页情感咨询情感美文情感百科情感生活学习充电旧版美文

标题	多值逻辑
类别	哲学
释义	多值逻辑 many-valued logic 一种非古典逻辑。与“二值的古典逻辑”相对。讨论命题具有“真”值、“假”值和其他值的逻辑。它可以具三个或三个以上的真值。多值逻辑的历史最早可以追溯到亚里士多德。20世纪初的麦柯尔(Scotman Hugh MacColl， 1837—1909)，皮尔斯、瓦西里耶夫(Н. А. Васильев，　1880—1940)则为多值逻辑的奠基人。麦柯尔就曾概述过一个除取传统的“真”、“假”外，也取必然、可能等模态值的命题逻辑系统。最早的多值逻辑系统是由卢卡西维茨和波斯特于20年代初提出。卢卡西维茨在分析关于将来偶然命题时注意到仅用真假二值来表述是不充分的。如：“明年12月21日中午我在华沙”这一陈述就是未定的，单用真假二值还不能对其表述，因此需用一种新的逻辑代替古典逻辑。赖辛巴赫从量子力学角度提供了支持卢卡西维茨三值逻辑的新证据。苏联逻辑学家鲍契瓦尔(Д.А.Бочвар)则出于克服语义悖论的需要设计了一种三值逻辑方案。克林在研究与数学证明有关问题时，为容纳不可判定的数学语句也提出需要构造新的三值逻辑。三值逻辑是最简单的多值逻辑。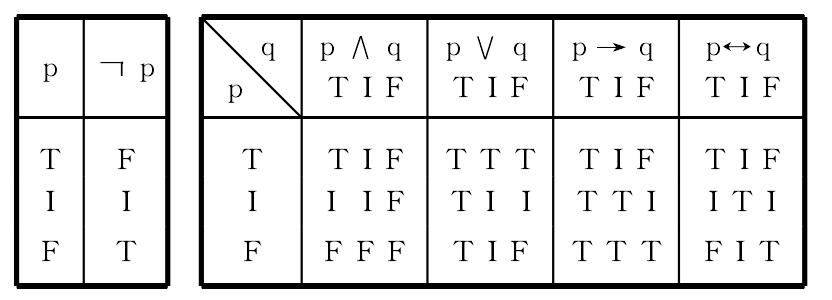卢卡西维茨三值逻辑系统L₃的特点表现在下述真值表上：在这真值表上，(1)有三个真值T、I、F，它们真的程度依次递减。(2)给定真值的一个语句的否定是它的“对立物”，中间值I的否定不变。(3)合取的真值取合取项中最假的。此时仅当合取项p、q都真时，合取式才真，这是继承了二值逻辑的规则。(4)析取的真值取析取项中最真的。此时仅当析取项p、q都假时，析取式才假，它也继承了二值逻辑值的规则。(5)蕴涵式“p→q”的真值与“p∨q”的真值相同，除“I→I”以外。(6)等值式“p↔q”的真值与“(p→q)∧(q→p)”的真值同。可以验证，在L₈中“p∨p”和“(p∧p)”并非永真，因此，矛盾律、排中律、同一律都不能成立。鲍契瓦尔和克林的三值逻辑系统也有与L₃不相同的真值表。
随便看	二乙基麦角酰胺二价释放者二位数组合研究二元正态分布二元论二分法二分法定理二列相关系数二十四诗品二型性二度创作二度空间二择一测验二本论二次分析二磷酸腺苷二类判断二级传播理论二级变化二级强化二级投射区二级获益二级行为二级驱力二者不可得兼 encapsulation molding encapsulation of a semiconductor device sensitive to radiation encapsulation of endoparasite encapsulation press encapsulation technique encapsulation technology encapsulation testing encapsulator encapsulators encapsule encapsulization encapsulted torpedo encaptivate encaptivated encaptivates 情书语录伤感是什么意思娉婷情感语录短句是什么意思情书字谜大全视频是什么意思有个性的情感文案句子是什么意思情感文案带图片下载是什么意思将进酒表达诗人情感的字词是什么意思快乐的情书图片大全是什么意思生活的情感语录文案是什么意思情书期待是什么意思婆媳之间隔阂情感文案是什么意思游子对家的情感表达有哪些是什么意思动漫情感语录配乐素材下载是什么意思被别人的爱情感动到的句子是什么意思侧逆光表达情感是什么意思散文情感题目怎么写的是什么意思曾经那么相爱，分手却变得陌生老公不愿意过夫妻生活是什么原因小时候，开心是本能。长大了，开心是本事男朋友不愿意和我结婚怎么办女朋友总是说分手怎么办老婆和我分床已经半年了，要和我离婚老公背叛我，我原谅不了他怎么办男朋友总是沉默应对我的问题老公不像个男人怎么办，我要离婚吗不想和公公婆婆住一起，怎么和他们说男朋友除了对我好没有任何优点男朋友不能接受自己的过去怎么办在教育孩子上和婆婆发生了争执怎么办夫妻常年不在一起生活，婚姻要怎么维持老婆管我管得太严了怎么办厦门早上游必去景点推荐探索宜兰：不可错过的必游景点推荐探索周口的魅力：必去景点全攻略杭州下雨天必去的五大景点【2024最新】珠海亲子游必去景点推荐，带宝宝畅玩一整天慈溪旅游攻略：五大必去景点推荐，让您玩转慈溪探索迪庆：不可错过的魅力景点推荐发现秦皇岛：不容错过的十大绝美旅游景点广州旅游攻略：最值得一游的景点推荐探索泰山：十大必游景点推荐探索重庆夜生活：十大必去夜景景点推荐探索合肥庐阳区：不可错过的必游景点推荐探索厦门鼓浪屿：绝对不能错过的景点推荐最值得一游的广州景点大揭秘探索西藏：不容错过的十大旅行景点

依恋情感网情感百科知识大全收录了49620条情感类百科知识词条，覆盖心理学、哲学、美学等领域，基本涵盖了日常生活中常见问题的详细解释，是情感生活的有利工具。