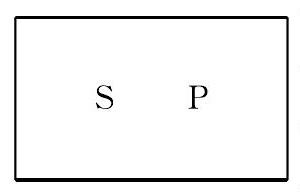
区别命题的一种。断定所有对象S具有P性质,并且断定所有具有P性质的对象都是S。和全称肯定命题不同,它是由两个全称肯定命题组合而成的复合命题,用“Aa”表示,命题的形式是:SAP∧PAS(两个支命题都是A命题,故用“Aa”表示)。断定了S和P的外延完全重合,即S=P。用图解表示(长方形表示论域)就是:
- Rorshach Inkblot Test
- Rorshach Test
- Rosenthal effect
- Rosenzweig Picture- frustration Study
- Ross Test of Higher Cognitive Processes
- rotation perception
- rote learning
- rote memorizing
- Rotter Incomplete Sentence Blank, RISB
- Rotter's Internal External Control Scale
- Rotter's Interpersоnal Trust Scale, RITS
- round window
- routine thinking training in sports
- routinized response behavior
- r-selection
- R-type cluster
- R-type factor analysis
- Rubin goblet profile figure
- rubrospinal tract
- Rudolph Hermann Lotze
- rule
- rule-consciousness
- rule-example method
- ruling type
- rumination
- locomotive station
- locomotive stock
- locomotive storage
- locomotive stored up
- locomotive supervise and record apparatus
- locomotive system
- locomotive technical specification
- locomotive temporary repair
- locomotive, tender
- Locomotive tender
- locomotive terminal
- locomotive test
- locomotive testing bed
- locomotive theory
- locomotive total wheel base
- 这一天是什么意思
- 这算什么是什么意思
- 不乖的女孩,一定要看喔!感谢生命中唯一的他是什么意思
- 天空下的love story【1】是什么意思
- 我突然 发现我学会了假装是什么意思
- 《笑谈-古韵风-词集》是什么意思
- 如火四月,曲终人散。是什么意思
- 静静的,在沉默中忘却一切。是什么意思
- 少女、少女,离别在即。是什么意思
- 炫舞小说:当冷情女遇上滥情男是什么意思
- 谢谢你的不珍惜是什么意思
- 随想录是什么意思
- 再伟大的爱情,也会败给现实(写的很现实)是什么意思
- 千年流转, 话离殇, 一纸离殇破红尘是什么意思
- 多少人败给了等待 (看看自己是否也是!!)是什么意思
- 为什么婚姻破裂,变心才是导致婚姻破裂的根本原因
- 遭遇丈夫背叛妻子不吵不闹,为了孩子怎样去挽回婚姻的句子
- 最能打动人心的情话,为了孩子怎样去挽回婚姻的句子
- 女朋友跟我提分手怎么挽回,分手后如何约女友出来
- 怎样才能经营好夫妻关系 能做到这几点就可以
- 怎样才能经营好夫妻关系?
- 女朋友跟你分手说什么挽留,3个方法教你挽回
- 女孩子说分手怎么挽回,和女孩子分手怎么追回来
- 女孩提出分手还能复合吗,和平分手意味着释然
- 女孩提出分手还能复合吗,分手后复合的最佳时期
- 女孩子分手需要多久才能放下
- 女孩子分手需要多久才能放下,分手后三个月男女心理
- 女生初恋分手后多久才能放下,女孩子分手需要多久才能放下
- 女方提的分手如何挽回
- 挽回婚姻的最好方法有哪些,夫妻彼此出轨如何挽回
- 夏季糖尿病患者如何合理饮食?
- 夏季养生中年人的饮食推荐
- 夏季养生饮品推荐:清爽解渴又健康的饮品图片
- 男性夏季养生茶推荐,帮助调理健康
- 夏季女性养生的秘籍:喝哪些汤最好
- 夏季糖尿病患者养生方案指南
- 夏季简单养生食谱大揭秘 | 精选8款清凉美食推荐
- 夏季养生|酷夏时节的运动,你知道选择哪个最适合吗?
- 夏季饮用什么茶最适合养生
- 夏季女性养生茶推荐
- 夏季男生养生之道:推荐几款适合夏季的养生品
- 孙俪夏季养生吃什么食物?健康饮食维持好颜值
- 夏季喝什么汤或粥最有营养
- 夏季囤什么虾才最美味又健康
- 夏季养生食物推荐,让你健康度过炎炎夏季