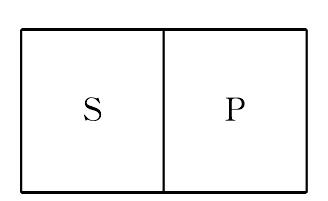
区别命题的一种。除断定所有对象S不具有性质P外,并还断定只有S不是P,即S和P的外延相加等于某一论域。和全称否定命题不同,它是一种复合命题,用“Ee”表示,命题的形式是:SEP∧PES∧S+P=1(“1”表示某一论域。两个支命题都是E命题,故用“Ee”表示)。也可简化为S=P。用图解表示(长方形表示论域)就是:
- optimal experience
- optimal foraging
- optimality currency
- optimality theory
- optimal mental state
- optimal movement
- optimal perceptual rate
- optimal period
- optimal stimulation level
- optimism
- optimum environment
- optimum load
- optimum state of performance
- optomotor feed back
- oral aggression complex
- oral anxiety
- oral character
- oral communication
- oral complex
- oral computation
- oral dependence character
- oral deprivation
- oral drive
- oral erotism
- oral fixation
- eletroanalytical chemistry
- eletroanesthesia
- eletroconductive resin
- eletrocute
- eletrodynamic vibrator
- eletroencephalograph
- eletrogustometer
- eletrokinetic potential
- eletrolyte
- eletrolyzable
- eletromagnetic type vibrometer
- eletromagnetic ware
- eletromallet condenser
- eletromechanical hammer
- eletrometric titration
- 繁华、落寞是什么意思
- 不要欺骗我,更不要拿我的感情当游戏是什么意思
- 相逢,不是恨晚,便是恨早。是什么意思
- 这四个字提醒我们要好好珍惜身边所有是什么意思
- 男人有男人的权利,女人有女人的权利是什么意思
- 不要迷恋哥,哥只是个传说是什么意思
- 有一中爱叫做懂得是什么意思
- 什么是我未来?是什么意思
- 伤心2009の诀别是什么意思
- 感情与心情是什么意思
- 最熟悉的陌生人②是什么意思
- 一个人脸上有太多的笑是因为心里有太多的痛…因为痛了,伪装笑了是什么意思
- 当你不理解一个人时,希望你不要伤他/她.................是什么意思
- 我该如何将你忘记≤网络的你≥是什么意思
- 完美并不美...是什么意思
- 遇到婚姻问题怎么办?妻子挽救婚姻的技巧
- 发生婚姻问题怎么解决?妻子挽回夫妻感情的方法
- 婚姻破裂后还有救吗?怎么挽救婚姻生活?
- 怎样爱一个人?征服男人的诀窍你了解这些吗?
- 怎样爱一个人?教你如何识别好男生和渣男
- 怎样爱一个人?你遇到家里逼婚的压力了吗
- 怎样爱一个人?你知道男人最喜欢的是什么类型的女人吗?
- 怎样爱一个人?他有女友却不时来挑逗我
- 怎样爱一个人?婚姻的本质是什么?
- 怎样爱一个人?如何留住男人的心?
- 怎样爱一个人?虚荣也是一种能量
- 怎样爱一个人?中国式“情人”
- 怎样爱一个人?教你如何辨别花心男
- 怎样爱一个人?如何让他知道我想和他谈恋爱
- 遇到婚姻问题怎么办?妻子改善夫妻感情的技巧
- 五通桥滑雪场-一场冬季狂欢的绝佳选择
- 探索阿鲁科尔沁旗滑雪胜地:推荐的滑雪场和精彩活动
- 探索中国北方最佳滑雪场——木垒县滑雪胜地推荐
- 北京房山附近的滑雪场推荐
- 万安山附近的滑雪场推荐
- 吉克普林滑雪场:发现滑雪者的天堂
- 七星岭滑雪场:推荐5家性价比高的酒店
- 阿尔卑斯山区滑雪胜地推荐
- 大石桥市滑雪场——冬季运动爱好者的绝佳选择
- 北京城区人造滑雪场盘点,带你一起领略冬日滑雪的乐趣
- 塞哈塔拉滑雪场周边推荐:美食、住宿和旅游景点
- 大明山滑雪场租赁店推荐——如何选择合适的滑雪装备和租赁店
- 成都闲暇好去处,推荐十大滑雪场
- 五峰滑雪场周边住宿推荐:舒适便利,让您的滑雪之旅更完美
- 探索昂昂溪区滑雪场的最佳选择