几何平均数geometric mean

几个变量值的连乘积的几次正方根， 以MG表示。在统计中，有许多统计量数系列是按几何级数来变异的，这种量数系列就叫做几何系列。几何平均数就是几何系列的中心量数。其计算公式为：

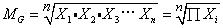
式中X₁,X₂,X3…X_n为各量数的取值；П是连乘的符号；n为总次数。如遇n较大，需要多次开方，计算较繁难时，通常可用对数来计算，上列公式可改写为：

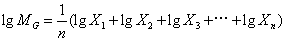
如在一组量数中，仅知初期数量，末期数量及期限，求各期平均发展速度时，表示平均发展速度的几何平均数等于各个环比发展速度的连乘积的n次正方根，即

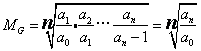
式中a₀为最初水平，a_n为最末水平，a₁/_a0,a₂/a₁等为环比发展速度，n为环比发展速度的个数。