x²检验chisquare test

运用服从x²分布的统计量进行的显著性检验。它是统计推断的早期方法之一，由英国统计学家皮尔逊(Pearson,K.)首创。它能同时检验多种数据（实验所得的次数分配）与某种理论次数分配的符合程度，也适用于其他计数资料，如等级、类别等的检验。计算X²的基本公式是：

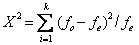
式中fo为观察次数，fe为理论次数，即期望次数。fo越接近fe，实际测得的数据与被检验的假设之间的一致性就越强，X²值就越小。反之，fo与fe之间的差数越大，X²值也就越大。根据X²检验的自由度：类别数(k-1)，和给定的显著性水平a，从X²分布表可查出相应的x²。当X²≥X²_a时，认为两者之间有显著差异；当X²≤X²_d时，则认为两者间无显著差异存在。X²检验的主要用途有：(1)比较落入特定类别的观察次数即计数资料的适合度的检验。(2)比较正态分布样本的观察方差与理论方差的差异。(3)作为概率组合的检验之用，也可用于分布检验等。