【随机变量条件分布】
拼译：conditional distribution of random variable
概率论术语。条件分布用于非独立随机变量的研究中。以二维情形为例，设(X，Y)是一个二维随机向量，它的联合分布函数为F(x，y)。则在已知Y=y0的条件下，X的条件分布函数F1(x｜Y=y0)=P(X≤x｜Y=y0)=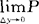
(X≤x｜y－Δy＜Y≤y+Δy)。同样，在已知X=x0的条件下，Y的条件分布函数F2(y｜X=x0)=P(Y≤y｜X=x0)=
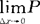(Y≤y｜x－Δx＜X≤x+Δx)。对于连续型随机变量，当边际密度函数f1(x0)≠0时，P(Y≤y｜X=x0)=
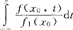，在给定X=x0的条件下，则Y的分布密度函数f2(y｜x0)=
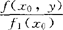为在X=x0的条件下Y的条件密度函数。同样，在Y=y0的条件下，X的条件密度函数为f1(x｜y0)=
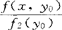，式中要求f2(y0)≠0。
- 神经递质
- 神经量子理论
- 神者生之本，形者生之具
- 神识
- 神话心理
- 神遇
- 神韵
- 禁令标志
- 禁必欲止
- 禁忌
- 禁戒综合征
- 禁欲主义
- 禁止训练
- 禁闭效应
- 禅
- 禅宗图文法
- 离中拟合指数
- 离婚咨询
- 离子通道
- 离巢雏鸟
- 离差
- 离差平方和
- 离差平方和法
- 离差智商
- 离异家庭子女心理
- Demilitarised zone
- demilitarization
- demilitarize
- demilitarized
- demilitarized zone
- demilitarized zone border
- DeMille
- De Mille
- De Mille, Agnes
- De Mille, Agnes George
- DeMille, Cecil B.
- De mille,Cecil Blount
- demilled
- demilles
- de milles
- 手写情书结尾文案是什么意思
- 英语情感语录男生是什么意思
- 情书365是什么意思
- 情书设置封面是什么意思
- 现实情感薄的句子简短是什么意思
- 忆苏散文的情感是什么意思
- 情感语录致女人的句子是什么意思
- 情感朗读文案视频是什么意思
- 画大饼情感语录短句子大全是什么意思
- 情感按钮毕淑敏散文精粹是什么意思
- 县城情感语录文案是什么意思
- 人参鸡汤语录情感文案是什么意思
- 歌曲吻别表达什么样的情感是什么意思
- 表达情感的短视频是什么意思
- 马未都情感语录是什么意思
- 泸州情感挽回咨询
- 跟对象约会的小技巧是什么
- 桂林婚姻家庭律师推荐咨询
- 情话用英语怎么说
- 见面约会小技巧
- 相亲遇到什么难忘的事情
- 凯源恋爱游戏攻略大全视频
- 舒涵讲情话
- 婚姻家庭法笔记知到智慧树
- 情话黄
- 老妈叫我相亲小视频大全
- 男友分手几天挽回了
- 慧眼讲婆媳关系
- 妻子挽回了婚姻的句子
- 挽回男朋友情感课程老师
- 夏季健康养生，这些水质适合多喝
- 夏季饮食养生，推荐五款清凉解暑的粥品
- 夏季养生的最佳时间
- 女性夏季养生饮食指南：健康新招助你度过炎热季节
- 夏季喝什么粥养生，告别暑湿从薏米粥开始
- 夏季出汗养生方法，让你健康过夏
- 夏季摆摊推荐的养生粥有哪些？
- 夏季养生花推荐：为您解析适宜用冷水浇的养生花品种
- 夏天养生的最佳选择：黄芪搭配四款饮品
- 夏季养生必备，这些食物让你消暑又滋补
- 夏季养生膏：为您带来清凉健康的享受
- 养生壶夏季煮什么食物有什么区别？
- 夏季喝养生白酒带来的好处
- 夏季绿茶搭配养生食材，健康养生更合理
- 夏季养生壶煮，解锁养颜瘦身新方式