【皮尔逊独立性卡方检验】
拼译:Pearson chi-square test of independence
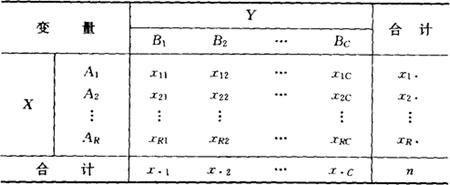
假设检验的一种。用于检验两个变量是否独立。皮尔逊卡方统计量的重要应用。X有R个表征值(状态)A1,A2,…,AR;Y有C个表征值:B1,B2,…,BC,二元类别变量(X,Y)定义在同一总体上。随机抽取n个个体,将观测资料汇总在R×C的列联表上(如下表)。欲检验的统计假设H0:X与Y是独立的;H1:H0不真。表中每格内数字xij是X取Ai且Y取Bj的次数,xi.= xij,x.j=
xij,x.j= xij,n=
xij,n= xi.=
xi.= x.j=
x.j= xij。检验统计量为χ2=
xij。检验统计量为χ2=
 ,在n→∞时,它的极限分布是χ2分布,自由度为(R-1)(C-1)。对给定的显著性水平α,查得χ2分布的右尾α分位点
,在n→∞时,它的极限分布是χ2分布,自由度为(R-1)(C-1)。对给定的显著性水平α,查得χ2分布的右尾α分位点 ;(R-1)(C-1)。当观测值
;(R-1)(C-1)。当观测值 >
> ;(R-1)(C-1)时,拒绝H0。这里的检验需要大样本。当R=C=2时,由上式给出的χ2统计量需要修正(称为雅茨连续性校正)为χ2=
;(R-1)(C-1)时,拒绝H0。这里的检验需要大样本。当R=C=2时,由上式给出的χ2统计量需要修正(称为雅茨连续性校正)为χ2= ,或用χ2统计量的简捷算法:χ2=
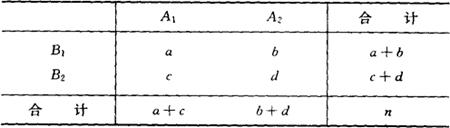
,或用χ2统计量的简捷算法:χ2= ,式中字母含义见2×2列联表所示。注意,此时χ2分布的自由度为1。
,式中字母含义见2×2列联表所示。注意,此时χ2分布的自由度为1。
R×C列联表
2×2列联表
- Spearman score model
- Spearman's rank correlation coefficient
- Spearman's rank correlation test
- specd-accuracy operating characteristic, SAOC
- special ability
- special aptitude test
- special chi1dren guidance clinic
- special class
- special column model
- special education
- special factor
- special group norm
- specialist-generalist continuum
- speciality of contact in commerce
- speciality of female consumer's purchase psychology and purchase action
- specialized perception
- specially gifted children
- special pedestrian
- special schoo1
- special skill of nation
- special talent
- species
- species recognition
- species specific behavior
- species specificity
- metrocentrism
- metrochrome
- metroclinal
- metroclinous hybrid
- metroclyst
- metroclyster
- metrocolpocele
- metrocoris esakii
- metrocorporation
- metrocorporis
- metrocracy
- metrocystosis
- metrocyte
- metrod
- Metrodin
- 网上情人,最好不要见面,就让它永远是个梦.是什么意思
- 其实、我还想爱是什么意思
- 请珍惜身边那个最关心自己的人是什么意思
- 爱老婆守则是什么意思
- 珍惜你身边那个爱生气的女人是什么意思
- 该来的还是来了是什么意思
- 分手了该怎么办?是什么意思
- 回头看下.那个深爱你的女孩是什么意思
- 忘记是什么意思
- 如果我再说爱你、你可否接受是什么意思
- 宝贝,你还好吗?是什么意思
- 只默默的付出 直至无味腐烂是什么意思
- 不是我的但很感人是什么意思
- 朋友真的会永远吗?是什么意思
- 留下,不代表还爱是什么意思
- 恋爱恐惧症是什么,该如何缓解?
- 男友分手后骂我很难听,为什么男生在分手之后骂女生
- 女人怎么挽回一个男人的心呢,挽回男人的正确方法
- 恋爱恐惧症是什么,如何消除对爱情的恐惧?
- 男友道歉女友最佳回复,男生道歉的时候女孩子应该怎么做
- 女人怎么才能挽回情感,挽回爱情的攻略
- 恋爱恐惧症是什么,你有恋爱恐惧症吗?
- 男友不耐烦的几种心理,怎么看出男朋友对你不耐烦了
- 和女人在分手后什么时候去挽回比较好
- 恋爱恐惧症有什么表现?这些中2条以上要留意了!
- 男生最喜欢什么礼物,送什么礼物男生会喜欢
- 恋爱恐惧症有什么表现,以下这些你中了几条?
- 女人越绝情越容易挽回吗,怎么挽回绝情的女人
- 男生追女生的套路,男生怎么追女生最快
- 恋爱恐惧症有什么表现,看看你中枪了吗?
- 王子岛亲子一日游攻略:玩转自然风光,尽享亲子时光
- 温江亲子游玩攻略:探索自然风光,体验乡村生活
- 探索海拉尔:亲子一日游精彩体验
- 探索温江周边亲子一日游的乐趣
- 杭州亲子一日游:探索正骨文化,感受城市魅力
- 上海台风天气下的亲子游玩攻略
- 探索大金华:亲子一日游精彩体验
- 华南京亲子一日游攻略:探索历史文化,感受城市魅力
- 宁波亲子游必去的5大室内景点推荐
- 西山岛亲子一日游攻略:探索自然风光,尽享亲子时光
- 探索佛山亲子乐园:室内游玩好去处推荐
- 上海亲子一日游:探索城市中的乐趣与惊喜
- 夏日亲子游玩攻略:五六月最佳目的地推荐
- 2023年9月最佳亲子旅游目的地推荐
- 探索揭阳周边亲子一日游胜地