【皮尔逊拟合优度检验】
拼译：Pearson goodness-of-fittest
亦称“拟合优度卡方检验”。非参数检验的一种。用于检验观测到的样本的频率分布与某一理论分布是否一致。皮尔逊提出。它使用χ2统计量，最简单古老，应用十分广泛。欲检验的假设是总体X服从某确定分布，如“H0：X服从二项分布”或“H0：X服从正态分布”。首先将X取值空间G划分为k个互不相交的子空间，即G=G1 UG2 U…U Gk，在H0成立的条件下，可求出X取值落人Gj的理论概率pj。现随机抽取大小为n的样本。于是X取值落入Gj的理论次数为npj，而观测次数记为fj。检验H0的统计量χ2=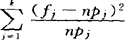
。由样本分布理论可知：当n→∞时，χ2的极限分布是自由度为k－1的χ2分布。在大样本情况下，对于显著性水平α，查得χ2分布的右侧α分位点
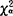(k－1)。若统计量的观测值
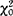大于
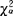(k－1)，则拒绝H0；否则，接受H0。使用时需注意两点：(1)n要求充分大，pj又不能太小。在实际中一般要求npj≥4，若某组的npj＜4，则该组可与邻组合并(j=1，2，…，k)。(2)检验统计量χ2中含有k个理论值pj，它们应当计算出来，但实际上并不容易。若有s个(s＜k)p值未知，可由样本去估计。这时统计量的自由度变为k－s－1。
- 《黄金史》
- 《黑格尔〈逻辑学〉一书摘要》
- 《黑格尔哲学中的活东西与死东西》
- 《黑格尔哲学批判》
- 《黑格尔宇宙论研究》
- 《黑格尔法哲学批判》
- 《黑格尔的再考察》
- 《黑格尔的秘密》
- 《默觚》
- 《齐民要术》
- 《齐物论》
- 《齐物论释》
- 《齐论》
- 《龙川文集》
- 《龟山集》
- 一
- 一
- 一一对应
- 一义性规律
- 一元
- 一元论
- 一元论历史观
- 一分
- 一分为二
- 一周而一不周
- beat together
- beat ... to it
- beat to it
- beat tone
- Beatton R.
- Beatton River
- Beat to Quarters
- beat to the draw
- beat to the punch
- beat ... to the punch
- be attracted by
- be attracted to
- be attract to
- be attributable to
- be attributed to
- 情感伤感文案馆是什么意思
- 明胶空心胶囊情书是什么意思
- 大哥歌曲表达的是什么情感是什么意思
- 驼铃表达什么情感是什么意思
- 河北夜听情感文章散文是什么意思
- 相约春天情感散文网文阅读是什么意思
- 植物表达情感图片大全集是什么意思
- 运命表达了什么情感特征是什么意思
- 情感爆发的散文短篇是什么意思
- 深度高级情感文案简短句子是什么意思
- 表达内心情感的小练笔是什么意思
- 幽默的情感语录图片是什么意思
- 堆积情感照片文案句子怎么写是什么意思
- 情感文案二选是什么意思
- 婚姻情感语录广场舞视频是什么意思
- 全校师生，全村人都瞧不起我，天天侮辱我骂我傻子垃圾
- 经历过地震，畏惧自然灾害，对未知感到恐惧，怎么办？
- 在最合适时想不起来该说什么，交流障碍，怎么办？
- 跟男友恋爱5个月了，婚前恐惧，该不该结婚？
- 为什么真实的我很难被接受？我到底是怎么了！
- 遇到被人喜欢也觉得很麻烦，想逃避，我怎么了？病了吗
- 老晨是谁？真的能带人上岸吗？
- 喜欢上同性的女同事，怎么才能情绪不受影响，怎么办？
- 有女友后，跟其他异性相处，避免说话等等，不正常是吗
- 快得抑郁症了，却又不敢跟父母说，怎么办？
- 有个让人压力比较大的朋友，沟通那么久都无果，怎么办
- 感觉我的父母控制欲很强，我该怎么办？反复沟通也没用
- 逃课，被老爸发现了，该不该被打屁股？
- 看到男友购物记录，看出来他对前任很好，控制不住生气
- 今天是失业第20天，容易因为失业而焦虑，怎么办？
- 探寻中山石岐区独具特色的网红小吃街
- 中国地方特色小吃手抄报——传统美食的独特魅力
- 中国江浙沪三地拥有丰富的特色小吃文化
- 东兴市特色小吃水果：品味南国美食文化
- 桂林特色小吃推荐：十款让你垂涎欲滴的美食
- 探寻北京海淀区特色小吃美食之旅
- 平顶山新华区必尝的特色小吃
- 沧州回民区独特美食，美味特色小吃推荐
- 江汉路地方特色小吃淘宝推荐
- 探索上海特色小吃的魅力——集合卡通图片的美食之旅
- 湖南特色小吃：辣得过瘾的美食大集合
- 探寻海坛特色小吃，品味食为福
- 伤心凉粉——江西南昌的特色小吃
- 探寻中国特色小吃：揭秘油泼面的由来和传统
- 石家庄特色美食：探寻街头巷尾的零食小吃美味