【概率密度函数】
拼译：probability density function
亦称“分布密度函数”，简称“密度函数”。概率论术语。描述连续型随机变量次数的函数。若连续型随机变量X存在非负可积函数f(x)(－∞＜x＜+∞)，且对一切实数x，其分布函数F(x)都可表达为F(x)=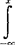
f(“)du，则称f(x)为X的概率密度函数。根据分布函数的性质可推导出密度函数f(x)具有下列性质：(1)f(x)≥0，－∞＜x＜+∞；(2)
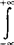f(x)dx=F(+∞)=1；(3)P(a＜x≤b)=F(b)－F(a)=
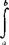f(x)dx。若知道一个连续型随机变量的密度函数，则可知道随机变量的全部概率密度1的分布情况。因此，连续型随机变量的分布类型通常都是以密度函数的表达式来定义的。参见“均匀分布”、“正态分布”。
- 治疗协议
- 治疗单元
- 治疗小组
- 治疗性双盲
- 治疗性社区
- 治疗结束
- 治疗者变量
- 沾光借影
- 法制心理学
- 法律家庭
- 泛化
- 泛心理论
- 泛性论
- 注意
- 注意分配
- 注意反应选择模型
- 注意增强
- 注意广度
- 注意稳定性
- 注意缺陷障碍
- 注意衰减模型
- 注意转移
- 注意过滤器模型
- 注意选择性
- 注意集中训练
- vision modulator
- vision monitoring
- vision monitoring equipment
- Vision,Monocular
- vision null
- vision obscure
- vision of left eye
- Vision of Love
- Vision of the Future
- vision on sound
- vision operation
- vision optical system
- vision output power
- vision package
- vision packing
- 关于张驰情感表达的密码的信息是什么意思
- 浪叔情感句子图片大全带字是什么意思
- 读冰心散文闲情感悟是什么意思
- 表达了他怎样的情感是什么意思
- 歌曲是表达情感的什么词是什么意思
- 密语情书激活卡是什么意思
- 即将分手情感文案是什么意思
- 自己拍情感段子文案短句是什么意思
- 农村情感热门文案是什么意思
- 朋友圈评价情感句子怎么写是什么意思
- 池上古诗表达诗人情感是什么意思
- 林清玄散文的情感是什么意思
- 关于爱情美好语录情感是什么意思
- 情感关系好句子app是什么意思
- 妈妈语录情感文字图片大全是什么意思
- 如何用“很爱她”挽回她的心？（15个必修的心理技巧让她重新爱上你）
- 两地分居的夫妻老公出轨的表现（如何发现老公出轨？）
- 三大星座男分手最绝情，这是为什么？（探究分手时最绝情的星座男及其特点，帮助你更好地了解他们。）
- 如何挽回摩羯座闺密（掌握这些技巧，让她重新回到你身边）
- 恋爱与单身（探究恋爱和单身的区别及其对生活的影响）
- 这个星座男生分手后不会开口说挽留（分手无需挽留，自由也是一种美好/星座分析）
- 如何以祝福过生日来挽回前女友？（挽回前女友的神秘法则大揭秘，祝福生日成功破局！）
- 成功挽回前男友的方法（一步步挽回男朋友的心，让爱情再次绽放）
- 以分分合合的爱情，我值得坚持！（坚定信念，破解关卡，赢得彼此信任。）
- 重建婚姻（面对婚姻中的挫折，如何重拾信任和爱情）
- 挽回前任后仍遭拒绝该怎么办？（如何正确应对挽回被拒绝的局面）
- 如何挽回女方父母的心理？（正确应对女方父母的反对和质疑，打破误解和隔阂，赢得信任和支持）
- 挽回被回避型依恋男友的有效方法（如何让你的男友重新爱上你）
- 挽回她的心，追回爱情！（如何成为她心中的唯一？——掌握情感挽回技巧）
- 分手后如何快速挽回男友（15个有效方法让你成功复合）
- 朗姆酒与白酒的区别及特点
- 酒后退烧药：喝了酒可以吃什么退烧药
- 这些水果和酒不能一起吃，为什么？
- 送老人礼物：百元价位下的优质酒品推荐
- 波本和黑麦可以调制出哪些经典鸡尾酒
- 酒10个月宝宝的辅食选择及建议
- 饮酒与什么食物不宜搭配
- 巽风台源酒发货时间及相关规定
- 昨天喝了酒胃疼喝什么药？如何缓解酒后胃疼？
- 揭秘三明永安人独爱的美酒
- 茅台酒取消订单为何难以抢购？解析茅台酒供需现状
- 揭秘酒一代的传奇人生：他究竟是怎样的人？
- 打造时尚搭配！酒红半身裙该怎么搭配打底裤？
- UGG酒红豆豆鞋搭配技巧，浅析适合的袜子颜色
- 哪种酒适合与酸奶搭配？酒和酸奶的完美组合！