【平方和分解】
拼译：partitioning of the sum of square
方差分析术语。在方差分析中将观测值发生的总变异，根据不同的变异源划分成几个部分的分解过程。数据的变异，是指数据组中每个数据与其平均数的离差平方和，即∑(Xi－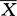
)2，记为SS。在最简单的单因素固定效应模型方差分析中，数据资料如下表。
单因素方差分析的数据资料
表中每一行数据是在同一个水平下得到的，其变异量称为组内变异或处理内变异，用平方和形式可表示为SSE=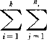
(Yij－
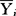)2，它反映的是在相同因素水平下得到的数据的变异，这个变异源只能归于随机误差e，故又称为误差平方和，记为SSE。表中各行数据间存在的变异量，用各组平均到全部数据的总平均之间的离差平方和表示，这个变异源可认为是因素的不同水平带来的，故称为组间平方和、处理平方和”或“因素平方和”，并记为SSA。SSA=
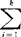ni(
－
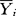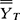)2，式中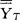
是总平均。全部数据的总变异用每个数据到总平均的离差平方和表示，即SST=
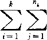(Yij－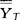
)2，称为总平方和。这样单因素固定效应模型的平方和分解就是SST=SSA+SSE，即总平方和等于因素平方和加误差平方和。
- concept
- concept acquisition
- concept assimilation
- concept attainment
- concept-driven processing
- concept extension
- concept formation
- concept identification
- conception development
- concept learning
- concept of middleness
- concept position of advertise ment
- concept storage
- concept structure
- conceptual compatibility
- conceptual implicit memory test
- conciliation
- concordance of offense
- concorde fallacy
- concrete art
- concrete attitude
- concrete behavior
- concrete-image thinking
- concrete knowledge
- concrete-operational stage
- vinylene monomer
- vinylene
- vinyle plastic
- Vinyl ester
- Vinylester
- vinyl ester, partially hydrolyzed
- vinyl ester polymer
- vinyl ester resin
- vinyl ester resins
- vinyl esters
- Vinylestrenolone
- vinyl ether
- Vinyl Ether Maleic Anhydride Polymer
- vinyl ether resin
- vinyl ethyl alcohol
- 模范情书高晓松是什么意思
- 情书写于花海和你是什么意思
- 情感短句高级爱情句子简短是什么意思
- 情书月季开几季是什么意思
- 云雾缭绕情感语录图片高清是什么意思
- 情感语录文案配音对话录音是什么意思
- 古诗文表达情感方式是什么意思
- 情书日本歌是什么意思
- 斜坡艾青诗选赏析表达情感是什么意思
- 截取学生情书是什么意思
- 朗读文章3分钟散文情感是什么意思
- 用景色表达情感的词语是什么意思
- 心情感恩文案短句干净是什么意思
- 小班艺术表达自己情感教案是什么意思
- 情感语录段子女版是什么意思
- 好玩点的表白方式
- 总裁相亲被保安打
- 中卫婚姻挽回专家咨询
- 蛇女能挽回婚姻吗知乎全文
- 女老板极力挽回婚姻
- 婚礼说唱歌
- 婆媳关系是最难相处
- 讲约会和撩妹技巧的
- 乔安齐飞相亲
- 相亲相爱什
- 为什么婆媳关系那么虚伪
- 李雪琴拒绝老板表白
- 土情话长胖
- 分手后怎么挽回前任男友
- 关于讲婚姻家庭的视频
- 南京周边8月亲子游好去处推荐
- 探寻台山沙滩上的亲子度假乐园
- 广东亲子游好去处推荐 - 带孩子玩转广东精彩体验
- 亲子游玩攻略：母女一起探索大自然的乐趣
- 泉州亲子游住宿攻略：最佳酒店民宿推荐
- 武汉亲子游旅行社精选推荐
- 成都动物园亲子游全攻略：探索动物奥秘,亲子互动乐无穷
- 亲子游玩攻略：1岁半宝宝的暑假趣味活动
- 亲子游玩好去处 - 2日游推荐攻略
- 三天亲子海边游玩攻略：让孩子玩个痛快
- 无锡周边亲子游好去处推荐 - 让孩子玩个痛快
- 芜湖周边亲子游好去处推荐 | 夏日避暑好去处
- 探秘川西自驾游，亲子出游的绝佳选择
- 汕头亲子一日游:探索海滨城市的自然与人文魅力
- 赤峰周边亲子游攻略：探索内蒙古大自然的魅力